Evaluación de hipótesis

Contrastes de hipótesis¶

Una hipótesis, en estadística, es una afirmación respecto a alguna característica de una población. Realizar un contraste de hipótesis supone comparar las predicciones con la realidad que observamos. Si existe coincidencia (con cierto margen de error), entonces aceptamos la hipótesis. En caso contrario, la rechazaremos.

Por ejemplo, cuando decimos que los chicos son más altos que las chicas, necesitamos obtener una conclusión matemática que nos permita asegurar que lo que suponemos es cierto. Esto se lleva a cabo con un contraste de hipótesis.

Pasos para formular un contraste de hipótesis¶

Las hipótesis son afirmaciones y podemos usar estadísticas para probarlas o refutarlas. El contraste de hipótesis estructura el problema para que podamos usar evidencias estadísticas para probar estas afirmaciones y verificarlas. Los pasos que seguiremos serán:

Definir la hipótesis.
Elegir el nivel de significación.
Verificar la hipótesis.
Decisión ¿Se acepta la hipótesis?

1. Definir la hipótesis¶

El contraste de hipótesis supondrá siempre una pregunta a la que estaremos buscando responder. La formulación de la pregunta sigue una estructura concreta y se construye a través de dos elementos: la hipótesis nula ( $H₀$ ) y la hipótesis alternativa ( $H₁$ ).

Hipótesis nula ( $H₀$ ): Es la hipótesis que sostiene que la suposición inicial que se tiene respecto a un parámetro poblacional es falsa. Por lo tanto, la hipótesis nula es aquella hipótesis que se pretende rechazar. Normalmente, va asociada con algún signo comparativo ("es igual a", "es menor o igual a" o "es mayor o igual a").
Hipótesis alternativa ( $H₁$ ): Es la hipótesis de la investigación que se pretende probar que es cierta. Es decir, la hipótesis alternativa es una suposición previa que tiene el investigador y para intentar demostrar que es verdadera llevará a cabo el contraste de hipótesis. Normalmente, se asocia con el signo comparativo contrario al de la hipótesis nula ("es diferente a", "es mayor a" o "es menor a").

2. Elegir el nivel de significación¶

El nivel de significación ( $α$ , alfa) hace referencia al grado de error que admitimos para aceptar o rechazar la hipótesis. Es la probabilidad de rechazar una hipótesis que en realidad es verdadera. En estadística, el nivel de significación se representa con el símbolo griego $α$ (alfa). Por eso también se conoce como nivel alfa.

Por ejemplo, si el nivel de significación es α=0,05, significa que la probabilidad de rechazar una hipótesis cuando es cierta es del 5%. En otras palabras, la probabilidad de hacer la estimación de un parámetro estadístico y equivocarnos con un error mayor al margen de error es del 5%.

Un nivel de significación del 0% implica que no hay ninguna duda de que la hipótesis aceptada es realmente verdadera. Sin embargo, un nivel de significación del 0% no existe en estadística, a menos que se haya analizado a toda una población, e incluso en tal caso no se puede estar totalmente seguro de que no se haya producido ningún error o sesgo durante la investigación.

3. Verificar la hipótesis¶

Una vez planteada la hipótesis nula, la hipótesis alternativa y el nivel de significación, tenemos que elegir el estadístico adecuado para este contraste de hipótesis. Hay muchas formas de hacerlo, pero las más utilizadas en el mundo real son el contraste de hipótesis para la media y el contraste de hipótesis para la proporción.

Antes de verificar la hipótesis debemos disponer de una muestra más o menos significativa de la población inicial. Esto es lo más importante del contraste de hipótesis. Esta muestra puede ser la población completa o no. Si por ejemplo queremos realizar un contraste de hipótesis para verificar si la media de la altura de los españoles es de 1,80 metros, realizaría el experimento sobre una población de 47 millones de personas. Esto es inabordable porque normalmente no se dispone de tanta información. Para ello, realizaremos un muestreo que es un subconjunto de esas 47 millones de personas y comparemos la media de 1,80 que hemos generalizado para la población y la media de la altura que se obtiene de la muestra, por ejemplo.

Para verificar la hipótesis, primero se calcula el Z-score, que es el valor que describe la posición de un valor individual dentro de una distribución de datos. El Z-score indica cuántas desviaciones estándar está un valor de la media de la distribución. Si el Z-score de un dato es 0, significa que el dato es igual a la media de la distribución. Si es positivo, indica que está por encima, y negativo, por debajo.

A partir del Z-score, se calcula el p-valor, que es una medida que se usa en estadística para ayudar a decidir si los resultados de una prueba son significativos o no. Es la probabilidad de obtener los resultados de tu experimento si la hipótesis nula fuera cierta. Si el p-valor es muy pequeño, significa que es muy poco probable obtener esos resultados si la hipótesis nula es cierta. Por lo tanto, concluimos que los resultados son significativos y rechazamos la hipótesis nula. En cambio, si el p-valor es grande, no podemos rechazar la hipótesis nula.

Contraste de hipótesis para la media¶

Este caso es uno de los más sencillos, el de comparación de dos medias, la nuestra y la de la población. Para compararlas, necesitamos previamente conocer la media y la desviación estándar de la población (nos vendrá dado porque estamos hipotetizando). La fórmula que caracteriza este cálculo es:

Z = {{\overline{x} - \mu} \over {{\sigma} \over {\sqrt{n}}}}

Donde $\overline{x}$ y $\sigma$ son la media y la desviación estándar de la población, $\mu$ es la media que calcularemos de la muestra y $n$ es el tamaño de la muestra.

Una vez se ha calculado el $Z-score$ de la prueba de hipótesis para la media, se calculará el $p-valor$ y se tomarán conclusiones:

Si el contraste de hipótesis era de desigualdad (la hipótesis alternativa asume que la media poblacional y muestral son diferentes), entonces se rechaza $H_0$ si $|Z| > Z_{\alpha/2}$ y se acepta $H_1$ .
Si el contraste de hipótesis era de "mayor que" (la hipótesis alternativa asume que la media poblacional es mayor que la muestral), entonces se rechaza $H_0$ si $Z > Z_{\alpha}$ y se acepta $H_1$ .
Si el contraste de hipótesis era de "menor que" (la hipótesis alternativa asume que la media poblacional es menor que la muestral), entonces se rechaza $H_0$ si $Z < -Z_{\alpha}$ y se acepta $H_1$ .

En el siguiente código nos planteamos si la media poblacional conocida (valor de 3) y la muestral son diferentes:

In [1]:

import numpy as np
import scipy.stats as stats

poblational_mean = 3
poblational_std = 0.5

sample = np.array([2.3, 2.9, 3.1, 2.5, 2.8, 3.0, 2.7])
sample_mean = np.mean(sample)
n = len(sample)

z_score = (sample_mean - poblational_mean) / (poblational_std / np.sqrt(n))
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))

print(f"Z-score value: {z_score}")
print(f"P-value: {p_value}")

Z-score value: -1.2850792082313751
P-value: 0.19876460637323423

Por lo tanto, rechazamos la hipótesis alternativa y aceptamos la hipótesis nula.

Contraste de hipótesis para la proporción¶

Este caso es uno de los más sencillos, el de comparación de dos proporciones, la nuestra y la de la población. Para compararlas, necesitamos previamente conocer la proporción de la población (nos vendrá dado porque estamos hipotetizando). La fórmula que caracteriza este cálculo es:

Z = {{\hat{p} - p} \over {\sqrt{{p(1-p)} \over {n}}}}

donde $p$ es la proporción propuesta, de la población, $\hat{p}$ es la proporción que calcularemos de la muestra, $n$ es el tamaño de la muestra y la raíz cuadrada incluyendo lo de dentro es la desviación estándar de la proporción.

Una vez se ha calculado el estadístico de la prueba de hipótesis para la proporción, se calculará también este valor para el nivel de significación previamente establecido ( $Z_\alpha$ ) y se compararán para aceptar o rechazar la hipótesis nula:

Si el contraste de hipótesis era de desigualdad (la hipótesis alternativa asume que la proporción poblacional y muestral son diferentes), entonces se rechaza $H_0$ si $|Z| > Z_{\alpha/2}$ y se acepta $H_1$ .
Si el contraste de hipótesis era de "mayor que" (la hipótesis alternativa asume que la proporción poblacional es mayor que la muestral), entonces se rechaza $H_0$ si $Z > Z_{\alpha}$ y se acepta $H_1$ .
Si el contraste de hipótesis era de "menor que" (la hipótesis alternativa asume que la proporción poblacional es menor que la muestral), entonces se rechaza $H_0$ si $Z < -Z_{\alpha}$ y se acepta $H_1$ .

En el siguiente código nos planteamos si la proporción poblacional conocida (valor de 3) y la muestral son diferentes. En este caso, la muestra consiste en valores de 1 y 0 porque estamos realizando un contraste de hipótesis para una proporción. Este tipo de prueba se utiliza a menudo en situaciones en las que se están comparando dos grupos o resultados que pueden clasificarse en dos categorías distintas.

In [2]:

import numpy as numpy
import scipy.stats as stats

poblational_proportion = 0.5

sample = np.array([1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0])
sample_proportion = np.mean(sample)
n = len(sample)

z_score = (sample_proportion - poblational_proportion) / np.sqrt((poblational_proportion * (1 - poblational_proportion)) / n)
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))

print(f"Z-score value: {z_score}")
print(f"P-value: {p_value}")

Z-score value: 0.44721359549995837
P-value: 0.6547208460185767

Por lo tanto, rechazamos la hipótesis alternativa y aceptamos la hipótesis nula.

4. Decisión. ¿Se acepta la hipótesis?¶

Dependiendo del objeto de la hipótesis y por lo tanto del proceso de verificación, se debe analizar el resultado y si se encuentra dentro del intervalo de confianza o no. Recordemos que el objeto de estudio es la hipótesis alternativa y en función del resultado podemos aceptar o rechazar la hipótesis nula.

El otro lado de los Contrastes de Hipótesis¶

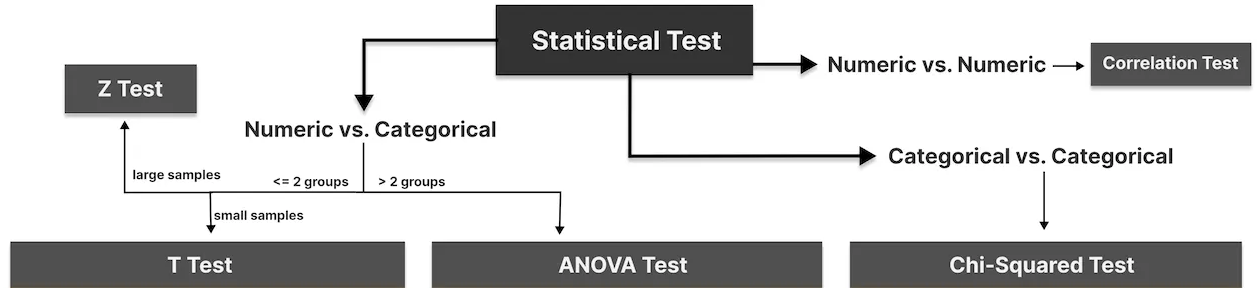
La ciencia detrás del estudio de hipótesis es muy amplia y aquí se ha ofrecido una información básica y necesaria para comprender sus fundamentos, pero no siempre se dan las condiciones tan favorables como se ha mostrado. Normalmente la varianza suele ser desconocida o queremos calcular la proporción de dos o más poblaciones. En este caso necesitamos recurrir a otras técnicas más avanzadas. Entre ellas, encontramos:

T-Test: Permite comparar dos grupos o categorías numéricas con un tamaño muestral reducido. Este caso es el contraste de hipótesis para la media en el caso de que se desconozca la varianza con muestra reducida. Sin embargo, también se puede usar cuando se conoce.
Z-Test: Permite comparar dos grupos o categorías numéricas con un tamaño muestral amplio. Este caso es el contraste de hipótesis para la media en el caso de que se desconozca la varianza con muestra amplia. Sin embargo, también se puede usar cuando se conoce.
ANOVA Test: Permite comparar dos o más grupos o categorías numéricas.
Chi-Cuadrado Test: Analiza la relación entre dos variables categóricas.
Correlation Test: Analiza la relación entre dos variables numéricas.

Diagrama de Contrastes de Hipótesis

Información más detallada: https://towardsdatascience.com/an-interactive-guide-to-hypothesis-testing-in-python-979f4d62d85