Hypothesis Testing

Hypothesis Testing¶

A hypothesis, in statistics, is a statement regarding some characteristic of a population. Performing a hypothesis test involves comparing the predictions with the reality we observe. If there is a match (with a certain margin of error), then we accept the hypothesis. If not, we reject it.

For example, when we say that boys are taller than girls, we need to obtain a mathematical conclusion that allows us to ensure that what we assume is true. This is done with a hypothesis test.

Steps to formulate a hypothesis test¶

Hypotheses are statements, and we can use statistics to prove or disprove them. Hypothesis testing structures the problem so that we can use statistical evidence to test these statements and verify them. The steps to follow will be:

Define the hypothesis.
Choose the level of significance.
Test the hypothesis.
Decision. Is the hypothesis accepted?

1. Define the hypothesis¶

Hypothesis testing will always involve a question that we will be seeking to answer. The formulation of the question follows a specific structure and is constructed through two elements: the null hypothesis ( $H₀$ ) and the alternative hypothesis ( $H₁$ ).

Null hypothesis ( $H₀$ ): This is the hypothesis that holds that the initial assumption regarding a population parameter is false. Therefore, the null hypothesis is the hypothesis that is intended to be rejected. It is usually associated with some comparative sign ("is equal to", "is less than or equal to", or "is greater than or equal to").
Alternative hypothesis ( $H₁$ ): This is the research hypothesis that is intended to be proven to be true. That is, the alternative hypothesis is a prior assumption that the researcher has, and to try to prove that it is true, he will carry out the hypothesis contrast. It is usually associated with the comparative sign opposite to that of the null hypothesis ("is different from", "is greater than", or "is less than").

2. Choose the significance level¶

The significance level ( $α$ , alpha) refers to the degree of error that we admit to accept or reject the hypothesis. It is the probability of rejecting a hypothesis that is actually true. In statistics, the significance level is represented by the Greek symbol $α$ (alpha). It is therefore also known as the alpha level.

For example, if the significance level is α=0.05, it means that the probability of rejecting a hypothesis when it is true is 5%. In other words, the probability of estimating a statistical parameter and being wrong with an error greater than the margin of error is 5%.

A significance level of 0% implies that there is no doubt that the accepted hypothesis is really true. However, a significance level of 0% does not exist in statistics unless an entire population has been analyzed, and even then, one cannot be absolutely sure that no error or bias has occurred during the investigation.

3. Testing the hypothesis¶

Having stated the null hypothesis, the alternative hypothesis, and the significance level, we have to choose the appropriate statistic for this hypothesis test. There are many ways to do this, but the most commonly used in the real world are hypothesis testing for the mean and hypothesis testing for the proportion.

Before testing the hypothesis, we must have a more or less significant sample of the initial population. This is the most important part of the hypothesis testing. This sample can be the whole population or not. If, for example, we want to perform a hypothesis test to verify whether the average height of Spaniards is 1.80 meters, we would perform the experiment on a population of 47 million people. This is unaffordable because normally there is not so much information available. To do this, we will sample a subset of those 47 million people and compare the mean of 1.80 that we have generalized for the population with the mean of the height obtained from the sample, for example.

To verify the hypothesis, we first calculate the Z-score, which is the value that describes the position of an individual value within a distribution of data. The Z-score indicates how many standard deviations a value is from the mean of the distribution. If the Z-score of a data is 0, it means that the data is equal to the mean of the distribution. If it is positive, it indicates that it is above, and if it is negative, it indicates that it is below.

From the Z-score, the p-value is calculated, which is a measure used in statistics to help decide whether the results of a test are significant or not. It is the probability of obtaining the results of your experiment if the null hypothesis were true. If the p-value is very small, it means that it is very unlikely to get those results if the null hypothesis is true. Therefore, we conclude that the results are significant and reject the null hypothesis. On the other hand, if the p-value is large, we cannot reject the null hypothesis.

Hypothesis testing for the mean¶

This is one of the simplest cases, that of comparing two means, ours and that of the population. To compare them, we first need to know the mean and the standard deviation of the population (this will be given to us because we are hypothesizing). The formula that characterizes this calculation is:

Z = {{\overline{x} - \mu} \over {{\sigma} \over {\sqrt{n}}}}

Where $\overline{x}$ and $\sigma$ are the mean and standard deviation of the population, $\mu$ is the mean that we will calculate from the sample, and $n$ is the sample size.

Once the $Z-score$ of the hypothesis test for the mean has been calculated, the $p-value$ will be calculated, and conclusions will be drawn:

If the hypothesis test was one of "inequality" (the alternative hypothesis assumes that the population and sample means are different), then $H_0$ is rejected if $|Z| > Z_{\alpha/2}$ and $H_1$ is accepted.
If the hypothesis test was "greater than" (the alternative hypothesis assumes that the population mean is greater than the sample mean), then $H_0$ is rejected if $Z > Z_{\alpha}$ and $H_1$ is accepted.
If the hypothesis test was "less than" (the alternative hypothesis assumes that the population mean is less than the sample mean), then $H_0$ is rejected if $Z < -Z_{\alpha}$ and $H_1$ is accepted.

In the following code, we ask whether the known population mean (value of 3) and the sample mean are different:

In [1]:

import numpy as np
import scipy.stats as stats

poblational_mean = 3
poblational_std = 0.5

sample = np.array([2.3, 2.9, 3.1, 2.5, 2.8, 3.0, 2.7])
sample_mean = np.mean(sample)
n = len(sample)

z_score = (sample_mean - poblational_mean) / (poblational_std / np.sqrt(n))
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))

print(f"Z-score value: {z_score}")
print(f"P-value: {p_value}")

Z-score value: -1.2850792082313751
P-value: 0.19876460637323423

Therefore, we reject the alternative hypothesis and accept the null hypothesis.

Hypothesis testing for the proportion¶

This is one of the simplest cases, that of comparing two proportions, ours and that of the population. To compare them, we first need to know the proportion of the population (it will be given to us because we are hypothesizing). The formula that characterizes this calculation is:

Z = {{\hat{p} - p} \over {\sqrt{{p(1-p)} \over {n}}}}

Where $p$ is the proposed proportion, from the population, $\hat{p}$ is the proportion we will calculate from the sample, $n$ is the sample size and the square root including the inside is the standard deviation of the proportion.

Once the hypothesis test statistic for the proportion has been calculated, this value will also be calculated for the previously established significance level ( $Z_\alpha$ ) and compared to accept or reject the null hypothesis:

If the hypothesis test was of inequality (the alternative hypothesis assumes that the population and sample proportion are different), then $H_0$ is rejected if $|Z| > Z_{\alpha/2}$ and $H_1$ is accepted.
If the hypothesis test was "greater than" (the alternative hypothesis assumes that the population proportion is greater than the sample proportion), then $H_0$ is rejected if $Z > Z_{\alpha}$ and $H_1$ is accepted.
If the hypothesis test was "less than" (the alternative hypothesis assumes that the population proportion is less than the sample proportion), then $H_0$ is rejected if $Z < -Z_{\alpha}$ and $H_1$ is accepted.

In the following code, we ask whether the known population proportion (value of 3) and the sample proportion are different. In this case, the sample consists of values between 1 and 0 because we are performing a hypothesis test for a proportion. This type of test is often used in situations where two groups or outcomes that can be classified into two different categories are being compared.

In [2]:

import numpy as numpy
import scipy.stats as stats

poblational_proportion = 0.5

sample = np.array([1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0])
sample_proportion = np.mean(sample)
n = len(sample)

z_score = (sample_proportion - poblational_proportion) / np.sqrt((poblational_proportion * (1 - poblational_proportion)) / n)
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))

print(f"Z-score value: {z_score}")
print(f"P-value: {p_value}")

Z-score value: 0.44721359549995837
P-value: 0.6547208460185767

Therefore, we reject the alternative hypothesis and accept the null hypothesis.

4. Decision. Is the hypothesis accepted?¶

Depending on the object of the hypothesis and therefore on the verification process, the result must be analyzed to determine whether it is within the confidence interval or not. Recall that the object of the study is the alternative hypothesis, and depending on the result, we can accept or reject the null hypothesis.

The other side of Hypothesis Testing¶

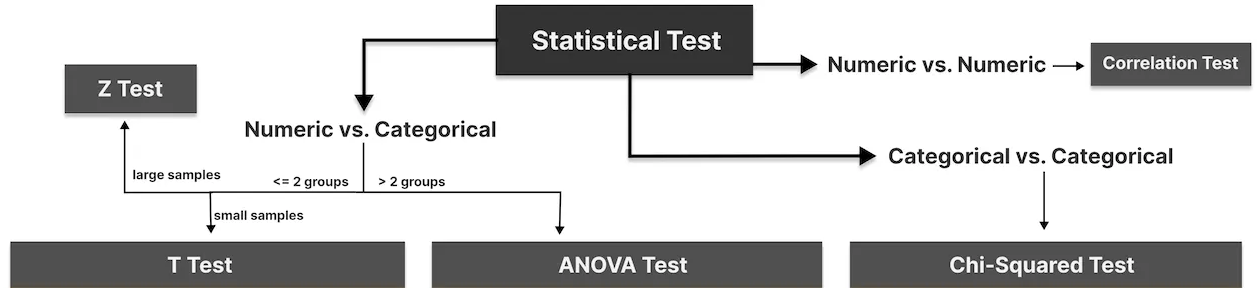
The science behind the study of hypotheses is very broad, and here we have provided some basic and necessary information to understand its fundamentals, but the conditions are not always as favorable as we have shown. Usually the variance is unknown, or we want to calculate the ratio of two or more populations. In this case, we need to resort to other, more advanced techniques. Among them, we find:

T-T-Test: Comparison between two groups or numerical categories with a reduced sample size. This case is the hypothesis test for the mean in the case where the variance is unknown with a reduced sample. However, it can also be used when it is known.
Z-Test: Comparison between two groups or numerical categories with a large sample size. This case is the hypothesis test for the mean in the case where the variance is unknown with a large sample. However, it can also be used when it is known.
ANOVA Test: Comparison between of two or more groups or numerical categories.
Chi-Square Test: Analyzes the relationship between two categorical variables.
Correlation Test: Analyzes the relationship between two numerical variables.

Hypothesis Testing Diagram

More detailed information: https://towardsdatascience.com/an-interactive-guide-to-hypothesis-testing-in-python-979f4d62d85