Python

Numpy

Machine Learning

Probability and Statistics

Linear Algebra

Álgebra Lineal

Álgebra Lineal¶

El álgebra lineal (linear algebra) es la rama de la matemática sobre ecuaciones lineales que utiliza espacio vectorial y matrices.

Las dos entidades matemáticas primarias que son de interés en álgebra lineal son el vector y la matriz. Son ejemplos de una entidad más general conocida como tensor. Los tensores poseen un orden (o rango), que determina el número de dimensiones en una matriz requerida para representarlo.

Vectores: Conjunto de elementos numéricos de un tamaño concreto y unidimensionales. Por ejemplo:

\begin{matrix} 3 \\ 4 \\ 5 \end{matrix}

numpy es la librería por excelencia para trabajar con estas estructuras de datos. Algunos ejemplos para generar vectores aleatorios son:

In [1]:

import numpy as np

# Vector de 10 unos
a1 = np.ones(10)
print(a1)

# Vector de 10 números que tienen la misma distancia entre sí, empezando por el 3 y acabando por el 15
a2 = np.linspace(3, 15, 10)
print(a2)

# Vector de 10 números aleatorios entre [0, 1)
a3 = np.random.rand(10)
print(a3)

# Vector de 10 números aleatorios entre [1, 10)
a4 = np.random.randint(1, 10, size=10)
print(a4)

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 3.          4.33333333  5.66666667  7.          8.33333333  9.66666667
 11.         12.33333333 13.66666667 15.        ]
[0.12715942 0.3056227  0.71055388 0.44321445 0.35334492 0.51475536
 0.04955689 0.94457741 0.30782969 0.73833549]
[7 4 9 5 5 8 7 6 6 6]

Matriz: Conjunto de vectores que conforman una estructura rectangular con filas y columnas. Por ejemplo:

\begin{matrix} 3 & 4 \\ 5 & 6 \end{matrix}

Con numpy también se puede trabajar para generar matrices. Algunos ejemplos para generarlas son:

In [2]:

# Matriz identidad de 5x5 (5 filas, 5 columnas)
m1 = np.identity(5)
print(m1)

# Matriz de 3x2 (3 filas, 2 columnas) con números aleatorios entre [0, 1)
m2 = np.random.rand(3, 2)
print(m2)

# Matriz de 7x5 (7 filas, 5 columnas) con números aleatorios entre 5 y 19
m3 = np.random.randint(5, 19, size=(7, 5))
print(m3)

[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]
[[0.08351724 0.12576021]
 [0.66183613 0.7666305 ]
 [0.87509394 0.05511234]]
[[17 10 11 10 15]
 [17 17  7 12 15]
 [17  8  6  9 15]
 [15 11 14 14 18]
 [16 17 15 10 10]
 [12 15 15 10  8]
 [ 6 10 11 18  6]]

Tensores: Los tensores son una matriz de números o funciones que se transmutan con ciertas reglas cuando cambian las coordenadas. Normalmente, el trabajo con tensores es más avanzado y requiere de librerías más orientadas al Machine Learning y a los modelos como TensorFlow o PyTorch.

El Machine Learning es el punto de contacto para Ciencias Informáticas y Estadística.

Vectores¶

Dado que los escalares existen para representar valores, ¿por qué son necesarios los vectores? Uno de los principales casos de uso de los vectores es representar cantidades físicas que tienen tanto una magnitud como una dirección. Los escalares solo son capaces de representar magnitudes.

Por ejemplo, los escalares y los vectores marcan su diferencia entre la rapidez de un automóvil y su velocidad. La velocidad contiene no solo su rapidez, sino que también su dirección de viaje.

En Machine Learning los vectores a menudo representan vectores de características, con sus componentes individuales especificando qué tan importante es una característica en particular. Tales características podrían incluir la importancia relativa de las palabras en un documento de texto, la intensidad de un conjunto de píxeles en una imagen bidimensional o valores de precios históricos para una muestra representativa de instrumentos financieros.

Operaciones Escalares

Las operaciones escalares involucran un vector y un número.

In [3]:

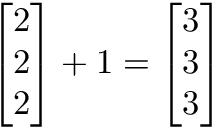
# Sumar un escalar y un vector. En el siguiente ejemplo, a cada elemento del vector se le sumará 2
a1 = np.array([1, 2, 3, 4])
print(a1 + 2)

# Restar un escalar y un vector. En el siguiente ejemplo, a cada elemento del vector se le restará 1
print(a1 - 1)

# Multiplicar un escalar y un vector. En el siguiente ejemplo, a cada elemento del vector se le multiplicará por 10
print(a1 * 10)

# Dividir un escalar y un vector. En el siguiente ejemplo, a cada elemento del vector se le dividirá entre 5
print(a1 / 5)

[3 4 5 6]
[0 1 2 3]
[10 20 30 40]
[0.2 0.4 0.6 0.8]

Multiplicación de vectores

Hay dos tipos de multiplicación vectorial: producto punto y producto de Hadamard.

El producto punto de dos vectores es un escalar. El producto punto de vectores y matrices (multiplicación de matrices) es una de las operaciones más importantes en el aprendizaje profundo.

In [4]:

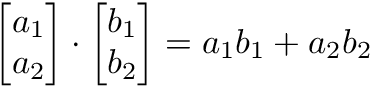
a1 = np.array([1, 2, 3, 4])
a2 = np.linspace(0, 20, 4)

a1.dot(a2)

Out[4]:

133.33333333333334

El producto de Hadamard es una multiplicación por elementos y genera un vector.

In [5]:

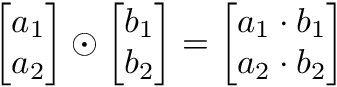
a1 = np.array([1, 2, 3, 4])
a2 = np.array([10, 10, 10, 10])

a1 * a2

Out[5]:

array([10, 20, 30, 40])

Matrices¶

Una matriz (matrix) es una cuadrícula rectangular de números o elementos (como una hoja de cálculo de Excel) con reglas especiales para sumar, restar y multiplicar.

Dimensiones de la matriz: Describimos las dimensiones de una matriz en términos de filas por columnas.

Operaciones escalares de matrices

Las operaciones escalares con matrices funcionan de la misma manera que con los vectores.

Simplemente, aplica el escalar a cada elemento de la matriz — suma, resta, divide, multiplica, etc.

In [6]:

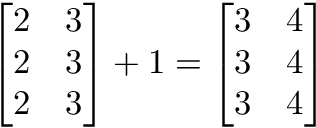
# Sumar un escalar y una matriz (en este caso de 2 filas y 4 columnas). En el siguiente ejemplo, a cada elemento de la matriz se le sumará 10
m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(m1 + 10)

# Restar un escalar y una matriz. En el siguiente ejemplo, a cada elemento de la matriz se le restará 5
print(m1 - 5)

# Multiplicar un escalar y una matriz. En el siguiente ejemplo, a cada elemento de la matriz se le multiplicará por 3
print(m1 * 3)

# Dividir un escalar y una matriz. En el siguiente ejemplo, a cada elemento de la matriz se le dividirá entre 2
print(m1 / 2)

[[11 12 13 14]
 [15 16 17 18]]
[[-4 -3 -2 -1]
 [ 0  1  2  3]]
[[ 3  6  9 12]
 [15 18 21 24]]
[[0.5 1.  1.5 2. ]
 [2.5 3.  3.5 4. ]]

Operaciones con matrices

Para sumar, restar o dividir dos matrices deben tener las mismas dimensiones. Combinamos los valores correspondientes de forma elemental para producir una nueva matriz.

In [7]:

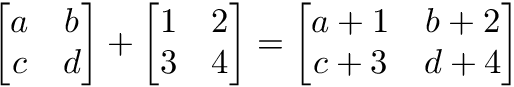
m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4, 6, 8], [-1, -2, -3, -4]])

# Sumar dos matrices. Deben tener la misma dimensión (mismo número de filas y de columnas). Se suman los elementos en la misma posición de la primera matriz y de la segunda
print(m1 + m2)

# Restar dos matrices. Deben tener la misma dimensión (mismo número de filas y de columnas). Se restan los elementos en la misma posición de la primera matriz y de la segunda
print(m1 - m2)

# Dividir dos matrices. Deben tener la misma dimensión (mismo número de filas y de columnas). Se dividen los elementos en la misma posición de la primera matriz y de la segunda
print(m1 / m2)

[[ 3  6  9 12]
 [ 4  4  4  4]]
[[-1 -2 -3 -4]
 [ 6  8 10 12]]
[[ 0.5         0.5         0.5         0.5       ]
 [-5.         -3.         -2.33333333 -2.        ]]

Multiplicación de matrices

Hay dos tipos de multiplicación de matrices: producto punto y producto de Hadamard.

El producto punto de dos matrices es una matriz con el número de filas de la primera y el número de columnas de la segunda. Tiene que haber igualdad entre el número de columnas de la primera y el número de filas de la segunda. Esto es, si la matriz "A" tiene unas dimensiones de $5$ x $3$ (5 filas y 3 columnas) y la matriz "B" unas dimensiones de $3$ x $2$ (3 filas y 2 columnas), la matriz resultante tras multiplicarlas tendrá unas dimensiones de $5$ x $2$ (y se pueden multiplicar porque la primera tiene 3 columnas y la segunda 3 filas).

En el producto punto de matrices, el elemento $c_{ij}$ de la matriz producto se obtiene multiplicando cada elemento de la fila $i$ de la matriz A por cada elemento de la columna $j$ de la matriz B y sumándolos.

In [8]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4], [6, 8], [-1, -2], [-3, -4]])

m1.dot(m2)

Out[8]:

array([[-1, -2],
       [15, 22]])

El producto de Hadamard de matrices es una operación elemental. Los valores que corresponden posicionalmente se multiplican para producir una nueva matriz.

In [9]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4, 6, 8], [-1, -2, -3, -4]])

m1 * m2

Out[9]:

array([[  2,   8,  18,  32],
       [ -5, -12, -21, -32]])

Transposición de matriz

La transposición de matriz proporciona una forma de "rotar" una de las matrices para que la operación cumpla con los requisitos de multiplicación y pueda continuar.

Hay dos pasos para transponer una matriz:

Rotar la matriz 90° a la derecha.
Invierte el orden de los elementos en cada fila (por ejemplo, $[a b c]$ se convierte en $[c b a]$ )

In [10]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])

m1.T

Out[10]:

array([[1, 5],
       [2, 6],
       [3, 7],
       [4, 8]])

In [11]:

m1.transpose()

Out[11]:

array([[1, 5],
       [2, 6],
       [3, 7],
       [4, 8]])

Aplicaciones del álgebra lineal¶

El álgebra lineal tiene un impacto directo sobre todos los procesos que involucren el tratamiento de datos:

Los datos en un dataset (conjunto de datos) están vectorizados. Las filas se insertan en un modelo una a la vez para realizar cálculos más fáciles y auténticos.
Todas las imágenes tienen una estructura tabular (matriz). Las técnicas de edición de imágenes, como recortar y cambiar de tamaño, utilizan operaciones algebraicas.
La regularización es un método que minimiza el tamaño de los coeficientes mientras los inserta en los datos.
El aprendizaje profundo funciona con vectores, matrices e incluso tensores, ya que requiere estructuras de datos lineales agregadas y multiplicadas.
El método 'One hot encoding' codifica categorías para facilitar las operaciones de álgebra.
En la regresión lineal, se utiliza álgebra lineal para describir la relación entre las variables.
Cuando encontramos datos irrelevantes, normalmente eliminamos las columnas redundantes, por lo que PCA actúa con la factorización de matrices.
Con la ayuda del álgebra lineal, los sistemas de recomendación pueden tener datos más depurados.