Python

Numpy

Machine Learning

Probability and Statistics

Linear Algebra

Edit on Github

Open in Colab

Linear Algebra

Linear Algebra¶

Linear algebra is the branch of linear equations mathematics that uses vector space and matrices.

The two primary mathematical entities that are of interest in linear algebra are the vector and the matrix. They are examples of a more general entity known as a tensor. Tensors possess an order (or rank), which determines the number of dimensions in a matrix required to represent it.

Vectors: A set of numerical elements of a particular size and one-dimensional. For example:

\begin{matrix} 3 \\ 4 \\ 5 \end{matrix}

numpy is the best library to work with these data structures. Some examples for generating random vectors are:

In [1]:

import numpy as np

# Vector of 10 ones
a1 = np.ones(10)
print(a1)

# Vector of 10 numbers that have the same distance from each other, starting with 3 and ending with 15
a2 = np.linspace(3, 15, 10)
print(a2)

# Vector of 10 random numbers between [0, 1)
a3 = np.random.rand(10)
print(a3)

# Vector of 10 random numbers between [1, 10)
a4 = np.random.randint(1, 10, size=10)
print(a4)

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 3.          4.33333333  5.66666667  7.          8.33333333  9.66666667
 11.         12.33333333 13.66666667 15.        ]
[0.11415076 0.19611812 0.8587248  0.36435106 0.62198295 0.0050302
 0.04972953 0.18915415 0.24093364 0.16267042]
[1 9 6 8 8 6 7 8 2 7]

Matrix: A set of vectors that form a rectangular structure with rows and columns. For example:

\begin{matrix} 3 & 4 \\ 5 & 6 \end{matrix}

With numpy you can also generate arrays. Some examples of how to generate them are:

In [2]:

# 5x5 Identity matrix (5 rows, 5 columns)
m1 = np.identity(5)
print(m1)

# 3x2 (3 rows, 2 columns) matrix with random numbers between [0, 1)
m2 = np.random.rand(3, 2)
print(m2)

# 7x5 matrix (7 rows, 5 columns) with random numbers between 5 and 19
m3 = np.random.randint(5, 19, size=(7, 5))
print(m3)

[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]
[[0.97199946 0.5296357 ]
 [0.69120675 0.36958526]
 [0.12795664 0.11455272]]
[[18 12  7 10 15]
 [16  5  8 16 13]
 [ 6 13 17 17 16]
 [ 6 15  9  7  9]
 [15  7 11 11 17]
 [18 12 11  5 11]
 [17  6 17  8 12]]

Tensors: Tensors are a matrix of numbers or functions that transmute with certain rules when the coordinates change. Usually, the work with tensors is more advanced and requires more Machine Learning and model-oriented libraries like TensorFlow or PyTorch.

Machine Learning is the contact point for Computer Science and Statistics.

Vectors¶

Since scalars exist to represent values, why are vectors necessary? One of the main use cases for vectors is to represent physical quantities that have both a magnitude and a direction. Scalars are only capable of representing magnitudes.

For example, scalars and vectors encode the difference between the speed of a car and its velocity. The velocity contains not only its speed, but also its direction of travel.

In Machine Learning, vectors often represent feature vectors, with their individual components specifying how important a particular feature is. Such features might include the relative importance of words in a text document, the intensity of a set of pixels in a two-dimensional image, or historical price values for a representative sample of financial instruments.

Scalar Operations

Scalar operations involve a vector and a number.

In [3]:

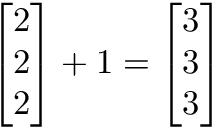
# Adding a scalar and a vector. In the following example, each element of the vector will have a 2 added to it
a1 = np.array([1, 2, 3, 4])
print(a1 + 2)

# Subtract a scalar and a vector. In the following example, each element of the vector will have a 1 subtracted from it
print(a1 - 1)

# Multiplying a scalar and a vector. In the following example, each element of the vector will be multiplied by 10
print(a1 * 10)

# Dividing a scalar and a vector. In the following example, each element of the vector will be divided by 5
print(a1 / 5)

[3 4 5 6]
[0 1 2 3]
[10 20 30 40]
[0.2 0.4 0.6 0.8]

Vector multiplication

There are two types of vector multiplication: dot product and Hadamard product.

The dot product of two vectors is a scalar. The dot product of vectors and matrices (matrix multiplication) is one of the most important operations in deep learning.

In [4]:

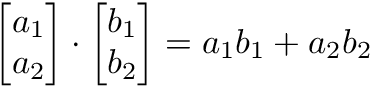
a1 = np.array([1, 2, 3, 4])
a2 = np.linspace(0, 20, 4)

a1.dot(a2)

Out[4]:

133.33333333333334

The Hadamard product is a multiplication by elements that generates a vector.

In [5]:

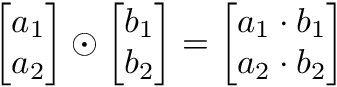
a1 = np.array([1, 2, 3, 4])
a2 = np.array([10, 10, 10, 10])

a1 * a2

Out[5]:

array([10, 20, 30, 40])

Matrices¶

A matrix is a rectangular grid of numbers or terms (like an Excel spreadsheet) with special rules for addition, subtraction, and multiplication.

Matrix dimensions: We describe the dimensions of a matrix in terms of rows by columns.

Scalar matrix operations

Scalar operations with matrices work the same way as with vectors.

You simply apply the scalar to each element of the matrix - add, subtract, divide, multiply, etc.

In [6]:

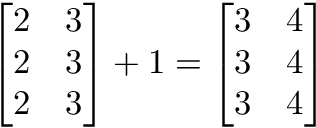
# Add a scalar and a matrix (in this case of 2 rows and 4 columns). In the following example, each element of the matrix will have a 10 added to it
m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(m1 + 10)

# Subtract a scalar and a matrix. In the following example, each element of the matrix will have a 5 subtracted from it
print(m1 - 5)

# Multiplying a scalar and a matrix. In the following example, each element of the matrix will be multiplied by 3
print(m1 * 3)

# Dividing a scalar and a matrix. In the following example, each element of the matrix will be divided by 2
print(m1 / 2)

[[11 12 13 14]
 [15 16 17 18]]
[[-4 -3 -2 -1]
 [ 0  1  2  3]]
[[ 3  6  9 12]
 [15 18 21 24]]
[[0.5 1.  1.5 2. ]
 [2.5 3.  3.5 4. ]]

Operations with matrix elements

To add, subtract or divide two matrices they must have the same dimensions. We combine the corresponding values in an elementary way to produce a new matrix.

In [7]:

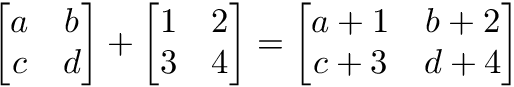
m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4, 6, 8], [-1, -2, -3, -4]])

# Add two matrices. They must have the same dimension (same number of rows and columns). The elements in the same position as the first matrix and the second matrix are added together
print(m1 + m2)

# Subtract two matrices. They must have the same dimension (same number of rows and columns). The elements in the same position as the first matrix and the second matrix are subtracted
print(m1 - m2)

# Split two matrices. They must have the same dimension (same number of rows and columns). The elements in the same position as the first matrix and the second matrix are divided
print(m1 / m2)

[[ 3  6  9 12]
 [ 4  4  4  4]]
[[-1 -2 -3 -4]
 [ 6  8 10 12]]
[[ 0.5         0.5         0.5         0.5       ]
 [-5.         -3.         -2.33333333 -2.        ]]

Matrix multiplication

There are two types of matrix multiplication: dot product and Hadamard product.

The dot product of two matrices is a matrix with the number of rows in the first matrix and the number of columns in the second matrix. There must be equality between the number of columns in the first and the number of rows in the second. That is, if matrix "A" has dimensions of $5$ x $3$ (5 rows and 3 columns) and matrix "B" has dimensions of $3$ x $2$ (3 rows and 2 columns), the resulting matrix after multiplying them will have dimensions of $5$ x $2$ (and they can be multiplied because the first one has 3 columns and the second one has 3 rows).

In the dot product of matrices, the element $c_{ij}$ of the product matrix is obtained by multiplying each element of row $i$ of matrix "A" by each element of column $j$ of matrix "B" and adding them together.

In [8]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4], [6, 8], [-1, -2], [-3, -4]])

m1.dot(m2)

Out[8]:

array([[-1, -2],
       [15, 22]])

The Hadamard product of matrices is an elementary operation. Positionally corresponding values are multiplied to produce a new matrix.

In [9]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
m2 = np.array([[2, 4, 6, 8], [-1, -2, -3, -4]])

m1 * m2

Out[9]:

array([[  2,   8,  18,  32],
       [ -5, -12, -21, -32]])

Matrix transpose

Matrix transposing provides a way to "rotate" one of the matrices so that the operation meets the multiplication requirements and can continue.

There are two steps to transpose a matrix:

Rotate the matrix 90° to the right.
Reverse the order of the elements in each row (e.g., $[a b c]$ becomes $[c b a]$ ).

In [10]:

m1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])

m1.T

Out[10]:

array([[1, 5],
       [2, 6],
       [3, 7],
       [4, 8]])

In [11]:

m1.transpose()

Out[11]:

array([[1, 5],
       [2, 6],
       [3, 7],
       [4, 8]])

Applications of linear algebra¶

Linear algebra has a direct impact on all processes involving data processing:

The data in a dataset is vectorized. Rows are inserted into a model one at a time for easier and more authentic calculations.
All images have a tabular (matrix) structure. Image editing techniques, such as cropping and scaling, use algebraic operations.
Regularization is a method that minimizes the size of coefficients while inserting them into the data.
Deep learning works with vectors, matrices and even tensors, as it requires aggregated and multiplied linear data structures.
The 'One hot encoding' method encodes categories to facilitate algebraic operations.
In linear regression, linear algebra is used to describe the relationship between variables.
When we find irrelevant data, we usually eliminate redundant columns, so PCA works with matrix factorization.
With the help of linear algebra, recommender systems can have more refined data.