Variables Aleatorias
Variables aleatorias¶
Una variable aleatoria (random variable) es una representación numérica de un evento aleatorio.
Tipos de variables aleatorias¶
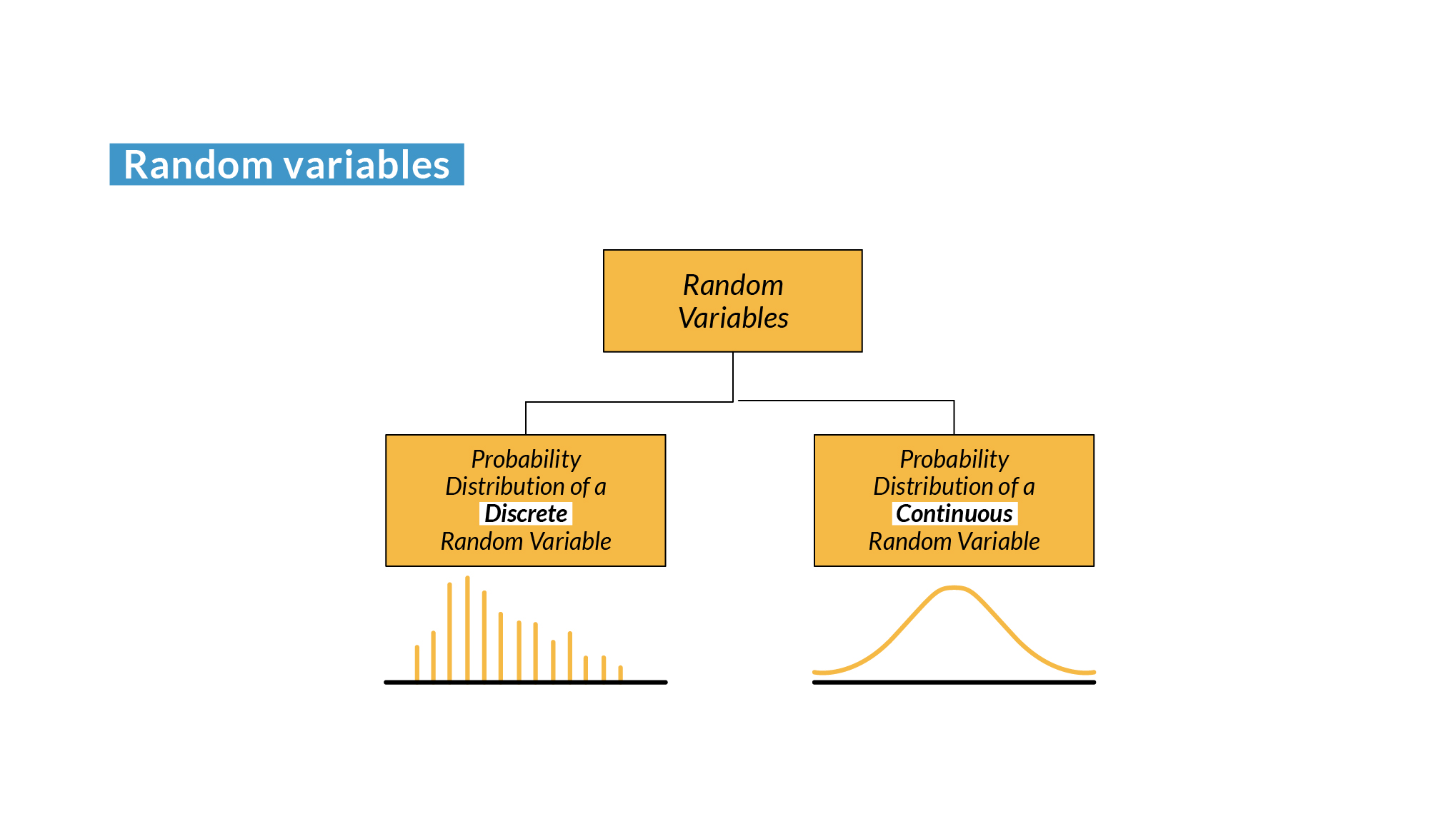
Debido a la naturaleza de los sucesos aleatorios, las variables pueden llegar a ser discretas o continuas.
- Variable aleatoria discreta (discrete random variable): Puede tomar un número finito contable de valores distintos. Por ejemplo, el número de veces que aparece cara al lanzar una moneda 10 veces es una variable aleatoria discreta, ya que puede tener valores como 0, 1, 2, ..., 10.
- Variable aleatoria continua (continuous random variable): Puede tomar cualquier valor en un intervalo continuo. Por ejemplo, la altura de una persona seleccionada al azar es una variable aleatoria continua porque puede ser cualquier valor dentro de un rango razonable, como entre 50 cm y 250 cm.
Cada variable aleatoria tiene asociada una función de distribución (distribution function), que describe la probabilidad de que la variable aleatoria tome un valor específico (para variables discretas) o caiga dentro de un intervalo específico (para las continuas).
Funciones de distribución¶
En estadística representamos una distribución de variables discretas a través de funciones de masa de probabilidad (PMF, probability mass function). El PMF define la probabilidad de todos los valores posibles de la variable aleatoria discreta. En variables aleatorias continuas, representamos su distribución por medio de la función de densidad de probabilidad (PDF, probability density function).
Función de masa de probabilidad¶
Es específica para variables aleatorias discretas y da la probabilidad de que la variable aleatoria tome un valor concreto.
import matplotlib.pyplot as plt
import numpy as np
data = np.arange(1, 7)
pmf = [1/6 for _ in data]
plt.figure(figsize = (10, 5))
plt.stem(data, pmf)
plt.title("PMF - Lanzar un dado")
plt.xlabel("Valor del dado")
plt.ylabel("Probabilidad")
plt.xticks(data)
plt.show()
En este caso vemos que la distribución de la variable aleatoria es uniforme, ya que sus probabilidades no cambian.
Función de densidad de probabilidad¶
Es específica para variables aleatorias continuas y es lo mismo que la PMF, pero para variables continuas.
from scipy.stats import norm
data = np.linspace(-5, 5, 1000)
pdf = norm.pdf(data)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf, "r-")
plt.title("PDF - Distribución normal")
plt.xlabel("Valor")
plt.ylabel("Densidad")
plt.show()
En este caso vemos que la distribución es normal, ya que el gráfico reproduce fielmente una campana gaussiana.
Función de distribución acumulativa¶
Una función de distribución acumulativa (CDF, cumulative distribution function) está definida para variables discretas y continuas y mide la probabilidad de que la variable aleatoria tome un valor menor o igual a uno dado.
data = np.linspace(-5, 5, 1000)
cdf = norm.cdf(data)
plt.figure(figsize = (10, 5))
plt.plot(data, cdf, "r-")
plt.title("CDF - Distribución normal")
plt.xlabel("Valor")
plt.ylabel("Probabilidad")
plt.show()
Si relacionamos las dos funciones anteriores:
data = np.linspace(-5, 5, 1000)
pdf = norm.pdf(data)
cdf = norm.cdf(data)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf, "r-")
plt.plot(data, cdf, "b-")
plt.xlabel("Valor")
plt.show()
Distribuciones de probabilidad¶
Las distribuciones de probabilidad (probability distributions) describen cómo están distribuidas las probabilidades de una variable aleatoria. Hay muchas distribuciones de probabilidad, y cada una describe un tipo diferente de proceso aleatorio.
Distribución Binomial¶
La distribución binomial (binomial distribution) aplica a variables aleatorias discretas y describe el número de éxitos en un conjunto de experimentos independientes de Bernoulli. Estos experimentos deben tener dos resultados posibles. Por ejemplo, número de caras obtenidas al lanzar una moneda 10 veces.
from scipy.stats import binom
n_experiments = 100
probability = 0.5
data = range(n_experiments)
pmf = binom.pmf(data, n_experiments, probability)
plt.figure(figsize = (10, 5))
plt.stem(data, pmf)
plt.show()
Distribución de Poisson¶
La distribución de Poisson (Poisson distribution) aplica a variables aleatorias discretas y describe el número de eventos que ocurren en un intervalo fijo de tiempo o espacio, dada una tasa promedio de ocurrencia. Por ejemplo, número de llamadas que recibe un call center en una hora.
from scipy.stats import poisson
n_experiments = 10
n_occur = 5
data = range(n_occur * n_experiments)
pmf = poisson.pmf(data, n_occur)
plt.figure(figsize = (10, 5))
plt.stem(data, pmf)
plt.show()
Distribución geométrica¶
La distribución geométrica (geometric distribution) aplica a variables aleatorias discretas y mide el número de ensayos necesarios para obtener el primer éxito en experimentos de Bernoulli independientes. Por ejemplo, número de lanzamientos de moneda necesarios para obtener la primera cara.
from scipy.stats import geom
n_experiments = 25
probability = 0.5
data = range(1, n_experiments)
pmf = geom.pmf(data, probability)
plt.figure(figsize = (10, 5))
plt.stem(data, pmf)
plt.show()
Distribución normal¶
La distribución normal (normal distribution) aplica a variables aleatorias continuas y tiene forma de campana, por eso se suele llamar también distribución Gaussiana. Está determinada por dos parámetros: la media y la desviación estándar . Por ejemplo, la distribución de alturas o pesos en una población grande.
from scipy.stats import norm
mu, sigma = 0, 1
data = np.linspace(-5, 5, 1000)
pdf = norm.pdf(data, mu, sigma)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf)
plt.show()
Distribución exponencial¶
La distribución exponencial (exponential distribution) aplica a variables aleatorias continuas y describe el tiempo entre eventos en un proceso de Poisson. Por ejemplo, el tiempo hasta que un dispositivo electrónico falle. Es la contraparte continua de la distribución geométrica.
from scipy.stats import expon
data = np.linspace(0, 5, 1000)
pdf = expon.pdf(data)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf)
plt.show()
Distribución uniforme¶
La distribución uniforme (uniform distribution) aplica a variables aleatorias continuas y supone que todos los valores en un intervalo tienen la misma probabilidad de ocurrencia. Por ejemplo, seleccionar un número al azar entre 0 y 1.
from scipy.stats import uniform
data = np.linspace(-2, 2, 1000)
pdf = uniform.pdf(data, loc = -1, scale = 2)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf)
plt.show()
Distribución Chi-cuadrada¶
La distribución Chi-cuadrada (Chi-square distribution) aplica a variables aleatorias continuas y es ampliamente utilizada para contrastes de hipótesis y tablas de contingencia.
from scipy.stats import chi2
df = 5
data = np.linspace(0, 20, 1000)
pdf = chi2.pdf(data, df)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf)
plt.show()
Distribución t de Estudiante¶
La distribución t de Estudiante (Student's t distribution) aplica a variables aleatorias continuas y es similar a la distribución normal pero con colas más pesadas. Es útil cuando el tamaño de la población es reducido.
from scipy.stats import t
data = np.linspace(-10, 10, 100)
pdf = t.pdf(data, df)
plt.figure(figsize = (10, 5))
plt.plot(data, pdf)
plt.show()
Cada una de estas distribuciones tiene su propio conjunto de parámetros y fórmulas asociadas. La elección de la distribución depende de la naturaleza del experimento o proceso que se esté modelando.