K Vecinos más Cercanos

K vecinos más cercanos (KNN)

El modelo K vecinos más cercanos (K-nearest neighbors), más conocido por sus siglas KNN es un algoritmo utilizado para tareas de clasificación y regresión. En KNN, un punto de datos se clasifica o se predice en función de la mayoría de las clases o valores de los K puntos de datos más cercanos en el espacio de características.

Por ejemplo, si quisiéramos predecir cuánto dinero gasta un cliente potencial en nuestro negocio, podríamos hacerlo en base a los 5 clientes más similares a él y promediar sus gastos para hacer la predicción.

Estructura

El modelo se construye en función de unos pasos bien delimitados y definidos, que son los siguientes:

1. Selección del valor de K: Se elige un valor para K, que representa el número de puntos de datos más cercanos que se considerarán para clasificar o predecir el nuevo punto de datos. Un valor pequeño puede llevar a un modelo más ruidoso y sensible a valores atípicos (outliers), mientras que un valor elevado puede facilitar la toma de decisión.
2. Medición de distancia: Se utiliza una métrica para calcular la distancia entre el punto de datos a clasificar o predecir y los demás puntos de datos en el conjunto de entrenamiento.
3. Identificación de los K vecinos más cercanos: Se seleccionan los K puntos de datos más cercanos (en función de la medición seleccionada).
4. Predicción: Si se trata de un problema de clasificación, el nuevo punto se clasifica en la clase más frecuente entre los K vecinos más cercanos. Si se trata de un problema de regresión, el valor objetivo para el nuevo punto se calcula como la media o la mediana de los valores de los K vecinos más próximos.

Además, el modelo no implica una fase de entrenamiento propiamente dicha, ya que todo el conjunto de entrenamiento se almacena en memoria para realizar las clasificaciones o predicciones en función de los vecinos más cercanos.

Es importante tener en cuenta que el rendimiento de este modelo puede depender en gran medida del valor de K y de la elección de la métrica de distancia. Además, puede ser computacionalmente costoso para grandes conjuntos de datos, ya que debe calcular la distancia con todos los puntos de entrenamiento para cada predicción:

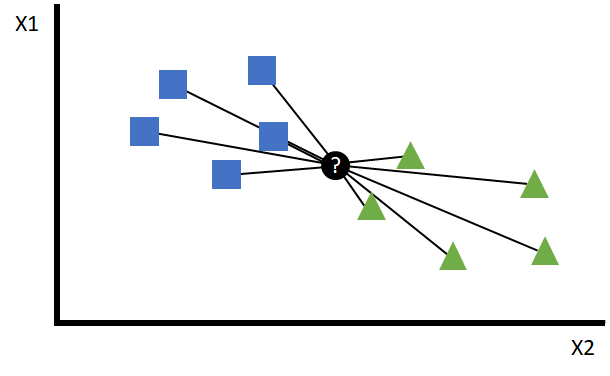
Esta distancia ordena a los puntos que rodean al punto que se quiere predecir, de tal forma que en función del valor de K se podrán elegir los más cercanos:

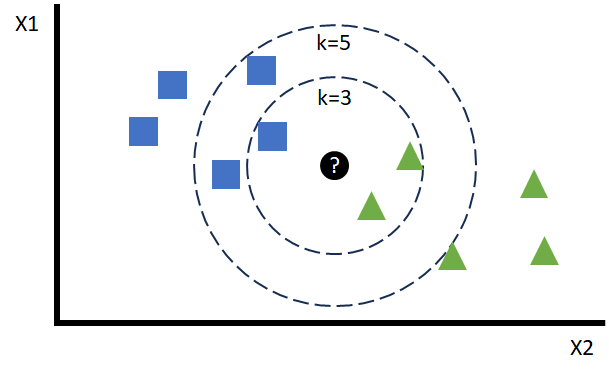
Una de las preguntas más comunes en este tipo de modelos trata sobre qué valor óptimo de K debemos elegir. Este número no se puede calcular a priori y se aproxima en la fase de optimización de hiperparámetros. Como se puede visualizar en el caso de la figura, su valor puede decantar una predicción concreta hacia la contraria u otra con ligeros cambios.

Métrica de distancia

Las métricas de distancia son funciones utilizadas para medir la proximidad o similitud entre dos puntos de datos en un modelo KNN. Existen una gran cantidad de propuestas, pero las más conocidas son las siguientes:

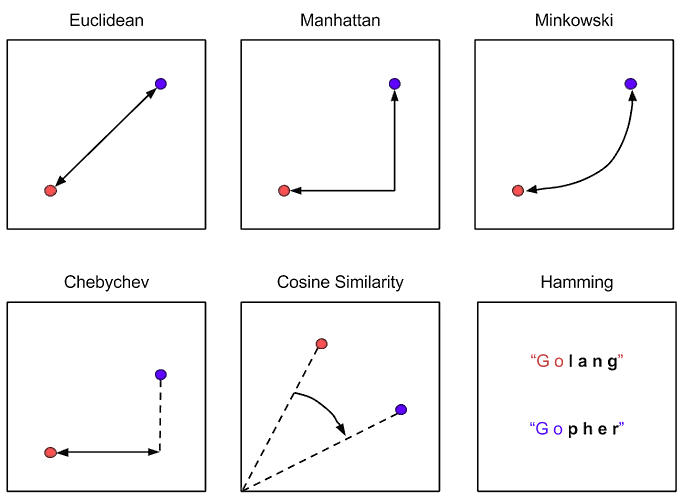
• Euclidiana (Euclidean): Mide la distancia en línea recta entre dos puntos. Adecuada para datos numéricos.
• Manhattan: Mide la distancia como la diferencia de las coordenadas cartesianas de ambos puntos. Es adecuada para datos numéricos también.
• Minkowski: Es un punto intermedio entre las dos anteriores.
• Chebyshev: También conocida como la distancia máxima entre la diferencia de alturas (eje Y) o de anchuras (eje X).
• Coseno (Cosine): Utilizada para medir la similitud entre dos vectores.
• Hamming: Se utiliza para datos categóricos o binarios. Mide la diferencia entre dos cadenas de caracteres de igual longitud.

Hiperparametrización del modelo

Podemos construir un modelo KNN fácilmente en Python utilizando la librería scikit-learn y las funciones KNeighborsClassifier y KNeighborsRegressor. Algunos de sus hiperparámetros más importantes y los primeros en los que debemos centrarnos son:

• n_neighbors: Es el valor K que hemos mencionado anteriormente. Representa el número de puntos de datos más cercanos que se considerarán al clasificar o predecir un nuevo punto de datos. Es el hiperparámetro más importante en KNN y afecta directamente la forma de las fronteras de decisión del modelo. Un valor pequeño puede llevar a un modelo más sensible al ruido y outliers, mientras que un valor grande puede simplificar el modelo.
• metric: Función para calcular la distancia entre los puntos de datos y el nuevo punto. La elección de la métrica puede afectar la forma en la que el modelo interpreta la proximidad entre puntos y, por lo tanto, la clasificación o predicción resultante.
• algorithm: Diferentes implementaciones del modelo KNN, que serán más o menos efectivos dependiendo de las características y complejidad del conjunto de datos.