← Regresar a lecciones
Abrir en Colab

Introduccion a Numpy

Logo de NumPy

Introducción a NumPy

NumPy es un juego de palabras que significa Python numérico (Numerical Python). Es una librería de código abierto que se utiliza para llevar a cabo tareas matemáticas con altísima eficiencia. Además, introduce estructuras de datos como los arrays multidimensionales, que se pueden operar entre ellos a alto nivel, sin meterse mucho en el detalle.

En concreto, las claves de esta librería son:

  • Array multidimensionales: Esta librería proporciona un objeto llamado ndarray, que permite almacenar y manipular grandes conjuntos de datos de forma eficiente. Los arrays pueden tener cualquier número de dimensiones.
  • Operaciones Vectorizadas: NumPy permite realizar operaciones matemáticas en arrays completos sin la necesidad de bucles explícitos en el código, lo que lo hace muy rápido y eficiente.
  • Funciones matemáticas: NumPy proporciona una amplia gama de funciones matemáticas para trabajar con arrays, incluyendo funciones trigonométricas, estadísticas, álgebra lineal, entre otras.
  • Eficiencia: Es mucho más rápido que la misma funcionalidad implementada directamente sobre Python nativo. Además, es muy flexible en términos de acceso y manipulación de elementos individuales o subconjuntos de arrays.

NumPy es una biblioteca fundamental para el Machine Learning y la ciencia de los datos en Python. Proporciona una amplia gama de herramientas y funciones para trabajar eficientemente con datos numéricos en forma de arrays y matrices.

Arrays

Un array de NumPy es una estructura de datos que permite almacenar una colección de elementos, generalmente números, en una o más dimensiones.

Array unidimensional

Un array unidimensional (1D) de NumPy es una estructura de datos que contiene una secuencia de elementos en una única dimensión. Es similar a una lista en Python, pero con las ventajas de rendimiento y funcionalidad que ofrece NumPy.

Array de una dimensión

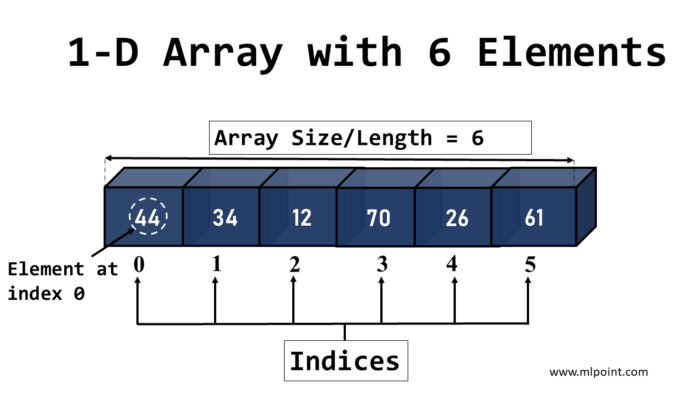
Un array 1D puede ser creado usando la función array de la librería con una lista de elementos como argumento. Por ejemplo:

In [1]:
import numpy as np

array = np.array([1, 2, 3, 4, 5])
array
Out[1]:
array([1, 2, 3, 4, 5])

Esto creará un array 1D con los elementos 1, 2, 3, 4 y 5. Los elementos del array deben ser del mismo tipo de datos. Si los elementos son de diferentes tipos, NumPy intentará convertirlos al mismo tipo si es posible.

En un array 1D, podemos acceder a los elementos usando índices (indexes), modificarlos y realizar operaciones matemáticas en el array completo de forma eficiente. A continuación se muestran algunas operaciones que se pueden realizar utilizando el array anterior:

In [2]:
# Acceder al tercer elemento
print(array[2])

# Cambiar el valor del segundo elemento
array[1] = 7
print(array)

# Sumar 10 a todos los elementos
array += 10
print(array)

# Calcular la suma de los elementos
sum_all = np.sum(array)
print(sum_all)

3
[1 7 3 4 5]
[11 17 13 14 15]
70

Array N-dimensional

Un array multidimensional o n-dimensional en NumPy es una estructura de datos que organiza elementos en múltiples dimensiones (ejes). Estos arrays permiten representar estructuras de datos más complejas, como matrices (array 2D, 2 ejes), tensores (array 3D, 3 ejes) y estructuras de mayor dimensión.

Arrays de diferentes dimensiones

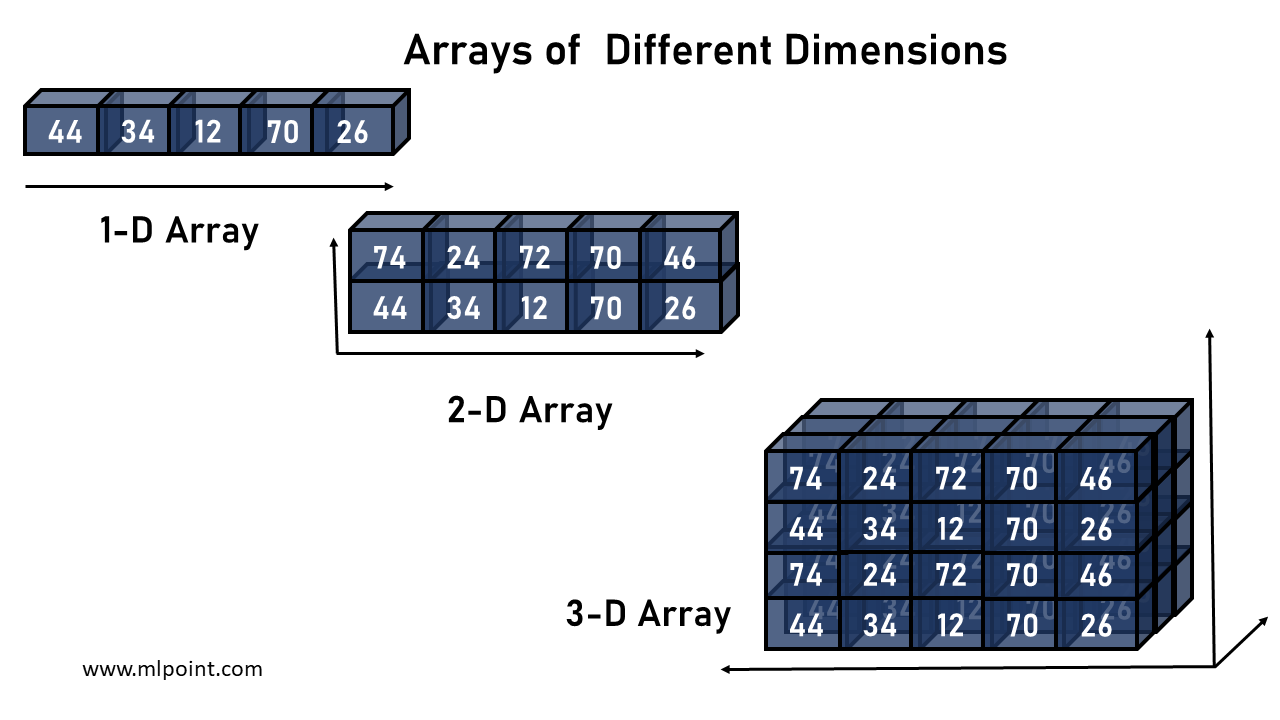
Un array N-dimensional puede ser creado también usando la función array de la librería. Por ejemplo, si queremos crear un array 2D:

In [3]:
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array_2d
Out[3]:
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

Si ahora quisiéramos crear un array 3D, tendríamos que pensar en él como una lista de matrices:

In [4]:
array_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
array_3d
Out[4]:
array([[[1, 2],
        [3, 4]],

       [[5, 6],
        [7, 8]]])

Al igual que sucedía con los arrays 1D, los elementos en un array multidimensional son accesibles mediante índices, se pueden realizar operaciones con ellos, etcétera.

A medida que agregamos más dimensiones, el principio básico sigue siendo el mismo: cada dimensión adicional puede considerarse como un nivel adicional de anidamiento. Sin embargo, a nivel práctico, trabajar con arrays de más de 3 o 4 dimensiones puede volverse más complejo y menos intuitivo.

Los arrays n-dimensionales en NumPy permiten una gran flexibilidad y potencia para representar y manipular datos en formas más complejas, especialmente útiles en campos como la ciencia de los datos, procesamiento de imágenes y aprendizaje profundo.

Funciones

NumPy proporciona una gran cantidad de funciones predefinidas y que se pueden aplicar directamente sobre las estructuras de datos vistas anteriormente o las propias de Python (listas, matrices, etcétera). Algunas de las más utilizadas en el análisis de datos son:

In [5]:
import numpy as np

# Crear un array para el ejemplo
arr = np.array([1, 2, 3, 4, 5])

# Operaciones Aritméticas
print("Suma:", np.add(arr, 5))
print("Producto:", np.multiply(arr, 3))

# Logarítmicas y Exponenciales
print("Logaritmo natural:", np.log(arr))
print("Exponencial:", np.exp(arr))

# Funciones Estadísticas
print("Media:", np.mean(arr))
print("Mediana:", np.median(arr))
print("Desviación estándar:", np.std(arr))
print("Varianza:", np.var(arr))
print("Máximo valor:", np.max(arr))
print("Índice del máximo valor:", np.argmax(arr))
print("Mínimo valor:", np.min(arr))
print("Índice del mínimo valor:", np.argmin(arr))
print("Suma de todos los elementos:", np.sum(arr))

# Funciones de Redondeo
arr_decimal = np.array([1.23, 2.47, 3.56, 4.89])
print("Redondeo:", np.around(arr_decimal))
print("Entero menor (floor):", np.floor(arr_decimal))
print("Entero mayor (ceil):", np.ceil(arr_decimal))

Suma: [ 6  7  8  9 10]
Producto: [ 3  6  9 12 15]
Logaritmo natural: [0.         0.69314718 1.09861229 1.38629436 1.60943791]
Exponencial: [  2.71828183   7.3890561   20.08553692  54.59815003 148.4131591 ]
Media: 3.0
Mediana: 3.0
Desviación estándar: 1.4142135623730951
Varianza: 2.0
Máximo valor: 5
Índice del máximo valor: 4
Mínimo valor: 1
Índice del mínimo valor: 0
Suma de todos los elementos: 15
Redondeo: [1. 2. 4. 5.]
Entero menor (floor): [1. 2. 3. 4.]
Entero mayor (ceil): [2. 3. 4. 5.]

Ejercicios: Haz clic en "open in colab" para realizarlos

Solución: https://github.com/4GeeksAcademy/machine-learning-prework/blob/main/02-numpy/02.1-Intro-to-Numpy_solutions.ipynb

Creación de arrays

Ejercicio 01: Crea un vector nulo (null vector) que tenga 10 elementos (★☆☆)

Un vector nulo es un array de una dimensión compuesto por ceros (0).

NOTA: Revisa la función np.zeros (https://numpy.org/doc/stable/reference/generated/numpy.zeros.html)

In [ ]:

Ejercicio 02: Crea un vector de unos que tenga 10 elementos (★☆☆)

NOTA: Revisa la función np.ones (https://numpy.org/doc/stable/reference/generated/numpy.ones.html)

In [ ]:

Ejercicio 03: Investiga la función linspace de NumPy y crea un array que contenga 10 elementos (★☆☆)

NOTA: Revisa la función np.linspace (https://numpy.org/doc/stable/reference/generated/numpy.linspace.html)

In [ ]:

Ejercicio 04: Busca varias formas de generar un array con números aleatorios y crea un array 1D y dos arrays 2D (★★☆)

NOTA: Revisa las funciones np.random.rand (https://numpy.org/doc/stable/reference/random/generated/numpy.random.rand.html), np.random.randint (https://numpy.org/doc/stable/reference/random/generated/numpy.random.randint.html) y np.random.randn (https://numpy.org/doc/stable/reference/random/generated/numpy.random.randn.html)

In [ ]:

Ejercicio 05: Crea una matriz (array 2D) identidad de 5x5 (★☆☆)

NOTA: Revisa la función np.eye(https://numpy.org/devdocs/reference/generated/numpy.eye.html)

In [ ]:

Ejercicio 06: Crea una matriz con números aleatorios de 3x2 y calcula el valor mínimo y máximo (★☆☆)

NOTA: Revisa la función np.min (https://numpy.org/devdocs/reference/generated/numpy.min.html) y np.max (https://numpy.org/devdocs/reference/generated/numpy.max.html)

In [ ]:

Ejercicio 07: Crea un vector con números aleatorios de 30 elementos y calcula la media (★☆☆)

NOTA: Revisa la función np.mean (https://numpy.org/doc/stable/reference/generated/numpy.mean.html)

In [ ]:

Ejercicio 08: Convierte la lista [1, 2, 3] y la tupla (1, 2, 3) en arrays (★☆☆)

In [ ]:

Operaciones entre arrays

Ejercicio 09: Invierte el vector del ejercicio anterior (★☆☆)

NOTA: Revisa la función np.flip (https://numpy.org/doc/stable/reference/generated/numpy.flip.html)

In [ ]:

Ejercicio 10: Cambia el tamaño de un array aleatorio de dimensiones 5x12 en 12x5 (★☆☆)

NOTA: Revisa la función np.reshape (https://numpy.org/doc/stable/reference/generated/numpy.reshape.html)

In [ ]:

Ejercicio 11: Convierte la lista [1, 2, 0, 0, 4, 0] en un array y obtén el índice de los elementos que no son cero (★★☆)

NOTA: Revisa la función np.where (https://numpy.org/devdocs/reference/generated/numpy.where.html)

In [ ]:

Ejercicio 12: Convierte la lista [0, 5, -1, 3, 15] en un array, multiplica sus valores por -2 y obtén los elementos pares (★★☆)

In [ ]:

Ejercicio 13: Crea un vector aleatorio de 10 elementos y ordénalo de menor a mayor (★★☆)

NOTA: Revisa la función np.sort (https://numpy.org/doc/stable/reference/generated/numpy.sort.html)

In [ ]:

Ejercicio 14: Genera dos vectores aleatorios de 8 elementos y aplica las operaciones de suma, resta y multiplicación entre ellos (★★☆)

NOTA: Revisa las funciones matemáticas: https://numpy.org/doc/stable/reference/routines.math.html

In [ ]:

Ejercicio 15: Convierte la lista [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] en un array y transfórmalo en una matriz con filas de 3 columnas (★★★)

In [ ]: