Árboles de Decisión

Árboles de Decisión

Un árbol de decisión (decision tree) es un modelo ampliamente utilizado en Machine Learning y que permite resolver problemas tanto de regresión como de clasificación. Es un modelo gráfico que imita la toma de decisiones humanas, es decir, se basa en una serie de preguntas para llegar a una conclusión.

La idea principal detrás de los árboles de decisión es dividir los datos en grupos cada vez más pequeños (llamados nodos) basándose en diferentes criterios hasta llegar a un resultado o decisión final. Estos criterios se seleccionan de tal manera que los elementos de cada nodo sean lo más similares posibles entre sí.

Estructura

La estructura de un árbol de decisión se asemeja a la de un árbol invertido. Comienza con un nodo llamado nodo raíz (root node) que contiene todos los datos. Este nodo se divide en dos o más nodos hijos basándose en algún criterio. Son los nodos de decisión (decision node). Este proceso se repite en cada nodo hijo, creando lo que se llaman ramas (branches), hasta que se llega a un nodo que no se divide más. Estos nodos finales se llaman nodos hoja (leaf nodes) y represen tan la decisión final o la predicción del árbol.

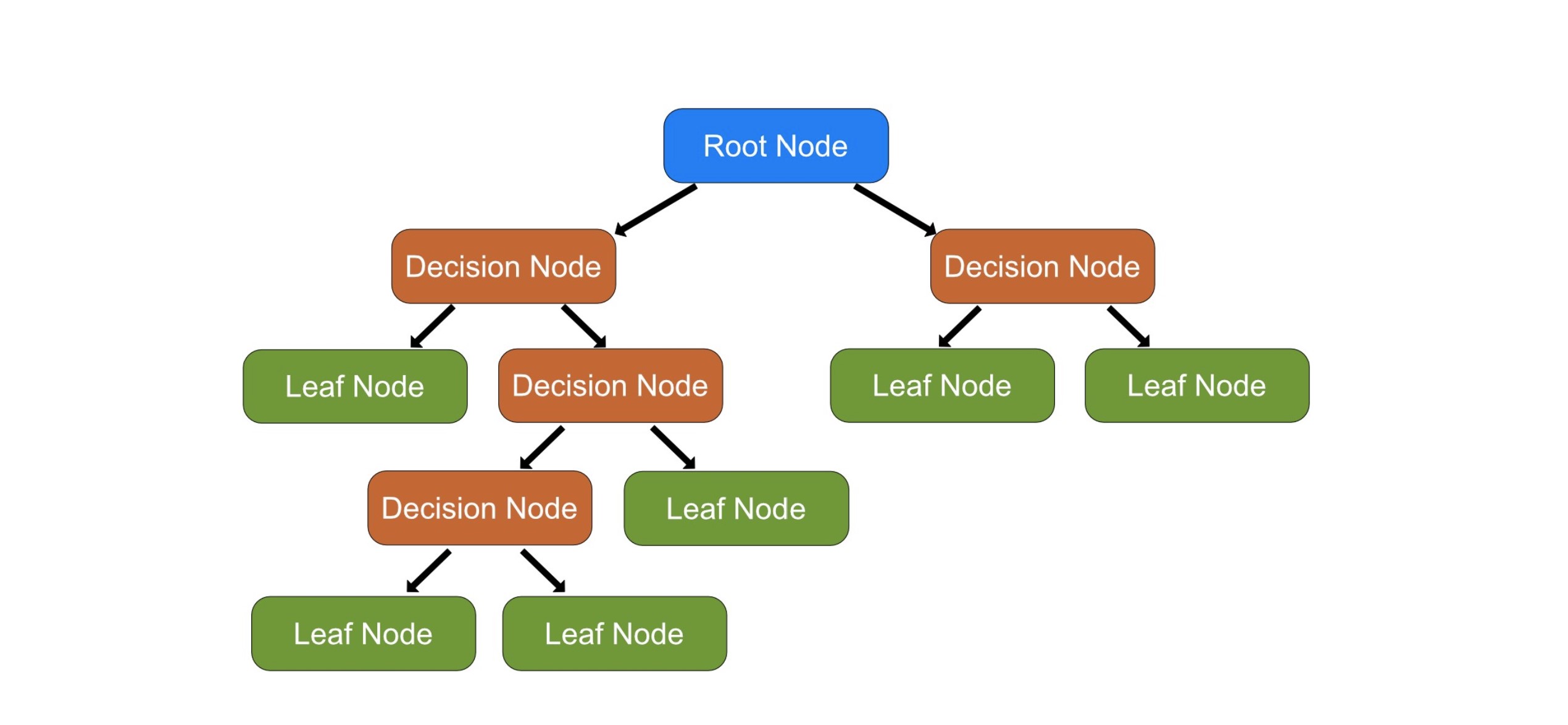
Un aspecto importante de los árboles de decisión es que son modelos muy interpretables. Puedes visualizar el árbol completo y seguir las decisiones que toma, lo cual no es posible en muchos otros tipos de modelos. Sin embargo, pueden ser propensos al sobreajuste, especialmente si el árbol se deja crecer demasiado.

Ejemplo de derivación

Imaginemos que estamos construyendo un árbol de decisión para decidir si debemos jugar al fútbol en función de las condiciones climáticas. Tenemos los siguientes datos:

Clima	Viento	¿Jugar al fútbol?
Soleado	Fuerte	No
Lluvioso	Débil	Sí
Soleado	Débil	Sí
Lluvioso	Fuerte	No

Empezamos con un único nodo que contiene todos los datos. Necesitamos decidir cuál será nuestro primer criterio de división, es decir, cuál de las dos características (Clima o Viento) deberíamos usar para dividir los datos. Este criterio se decide generalmente basándose en la pureza de los nodos resultantes. Para un problema de clasificación, un nodo es puro si todos sus datos pertenecen a la misma clase. En un problema de regresión, un nodo es puro si todos los datos de ese nodo tienen el mismo valor para la variable objetivo.

El objetivo de las divisiones en un árbol de decisión es aumentar la pureza de los nodos hijos. Por ejemplo, si tienes un nodo que contiene datos de emails spam y no spam, podrías dividirlo en base a si el email contiene la palabra "ganar". Esto podría aumentar la pureza si resulta que la mayoría de los emails que contienen la palabra "ganar" son spam y la mayoría de los que no la contienen son no spam.

En este caso, por simplicidad, supongamos que decidimos dividir por Clima primero. Entonces, dividimos los datos en dos nodos hijos: uno para los días soleados y otro para los días lluviosos:

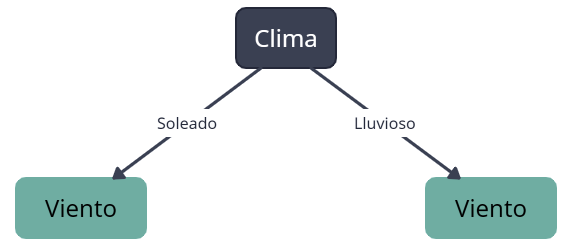
Ahora tenemos dos nodos hijos, cada uno con una parte de los datos:

• En el nodo "Soleado", tenemos los siguientes datos:

Clima	Viento	¿Jugar al fútbol?
Soleado	Fuerte	No
Soleado	Débil	Sí

• En el nodo "Lluvioso", tenemos los siguientes datos:

Clima	Viento	¿Jugar al fútbol?
Lluvioso	Débil	Sí
Lluvioso	Fuerte	No

Cada uno de estos nodos hijos se divide de nuevo, esta vez en función de la velocidad del viento:

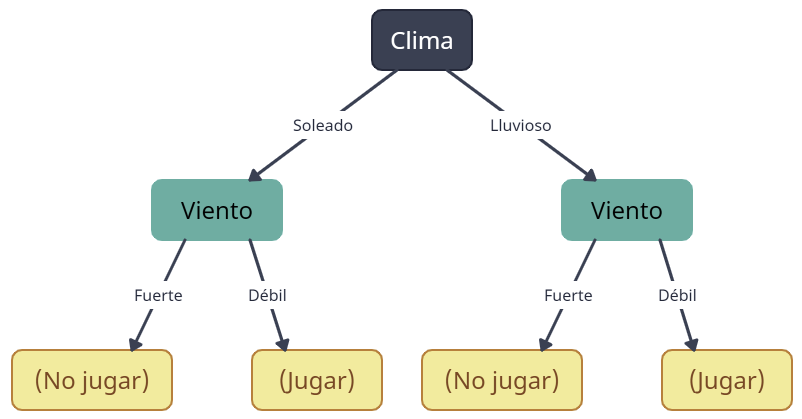
Ahora, cada uno de los nodos hijos (que ahora son nodos hoja, ya que no se dividirán más porque son puros) representa una decisión final basada en las condiciones climáticas. Por ejemplo, si el clima es soleado y el viento es débil, la decisión es jugar al fútbol.

Hiperparametrización del modelo

Podemos construir un árbol de decisión fácilmente en Python utilizando la librería scikit-learn y las funciones DecisionTreeClassifier y DecisionTreeRegressor. Algunos de sus hiperparámetros más importantes y los primeros en los que debemos centrarnos son:

• max_depth: La profundidad máxima del árbol. Esto limita cuántas divisiones puede tener, lo cual es útil para prevenir el sobreajuste. Si este valor es None, entonces los nodos se expanden hasta que las hojas sean puras o hasta que todas las hojas contengan menos muestras que min_samples_split.
• min_samples_split: El número mínimo de muestras necesarias para dividir un nodo. Si un nodo tiene menos muestras que min_samples_split, entonces no se dividirá, incluso aunque no sea puro. Ayuda a prevenir el sobreajuste.
• min_samples_leaf: El número mínimo de muestras que debe haber en un nodo hoja. Un nodo se dividirá si al hacerlo se crean al menos min_samples_leaf muestras en cada uno de los hijos. Esto también ayuda a prevenir el sobreajuste.
• max_features: El número máximo de características a considerar al buscar la mejor división. Si max_features es None, entonces se considerarán todas las características. Reducir este número puede hacer que el modelo sea más simple y rápido de entrenar, pero también puede hacer que pase por alto algunas relaciones importantes.
• criterion: La función para medir la calidad de una división. Dependiendo de la naturaleza del árbol (clasificar o regresar), las opciones varían. Este hiperparámetro es el encargado de elegir qué variable se va a ramificar.

Otro hiperparámetro muy importante es el random_state, que controla la semilla de generación aleatoria. Este atributo es crucial para asegurar la replicabilidad.