Que es una regresion lineal y para que utilizarla

Regresión Lineal

La regresión lineal (linear regression) es un tipo de modelo que se utiliza para predecir el valor de una variable dependiente (o variable objetivo) basado en el valor de una o más variables independientes (o variables predictoras). La regresión lineal presupone que existe una relación lineal directa entre las variables independientes y la variable dependiente. Si la relación entre la variable objetivo es con una única variable predictora, se dice que la regresión es simple. Si es con varias predictoras, recibe el nombre de regresión múltiple.

Este modelo se fundamenta en torno a cinco supuestos, que son los siguientes:

1. Linealidad: La variable objetivo y la(s) predictora(s) tienen una relación lineal.
2. Independencia: Las observaciones son independientes unas de otras.
3. Homoscedasticidad: La varianza de los errores (es decir, las diferencias entre las predicciones del modelo y los datos reales) es constante en todos los niveles de las variables independientes.
4. Normalidad de los errores: Los errores están normalmente distribuidos. Esto es importante para la realización de pruebas estadísticas y para construir intervalos de confianza.
5. Ausencia de multicolinealidad: En una regresión múltiple, las variables independientes no están perfectamente correlacionadas entre sí. Si hay correlación perfecta, se dice que los datos tienen multicolinealidad (hay variables que son iguales) y dificulta el cálculo de los coeficientes.

Qué es una Regresión Lineal Simple

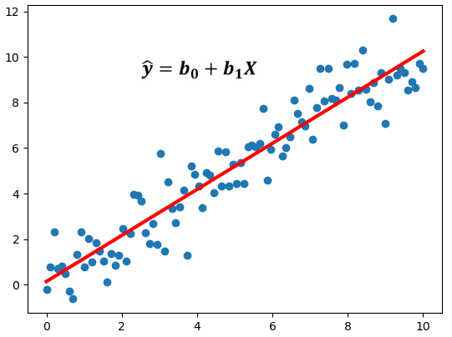
La regresión lineal simple permite estudiar las relaciones entre dos variables numéricas continuas. En este tipo de regresión intentamos ajustar una línea recta a los datos que mejor describa la relación entre las dos variables. Es decir, buscamos una línea que minimice la distancia vertical entre sí misma y todos los puntos de datos, de tal forma que la mejor relación lineal se da cuando todos los puntos conforman la recta y no existe dispersión.

La ecuación que define esta relación (recta) es:

$Y = a + bX + e$

Donde:

• $Y$ es la variable dependiente que intentamos predecir o modelar.
• $X$ es la variable independiente que utilizamos para hacer la predicción.
• $a$ y $b$ son los coeficientes que queremos que el modelo aprenda. $a$ es el intercepto (valor de $Y$ cuando $X$ es cero) y $b$ es la pendiente.
• $e$ es el error en la predicción comentado anteriormente. Es la diferencia entre el valor real de $Y$ y el valor de $Y$ predicho por el modelo.

El objetivo de la regresión lineal simple es, por lo tanto, encontrar los mejores valores de $a$ y $b$ que minimizan el error $e$. Una vez que hemos encontrado estos valores, podemos usarlos para predecir los valores de $Y$ dada cualquier $X$.

En la regresión lineal, cada valor dependiente tiene una sola variable independiente correspondiente.

Qué es una Regresión Lineal Múltiple

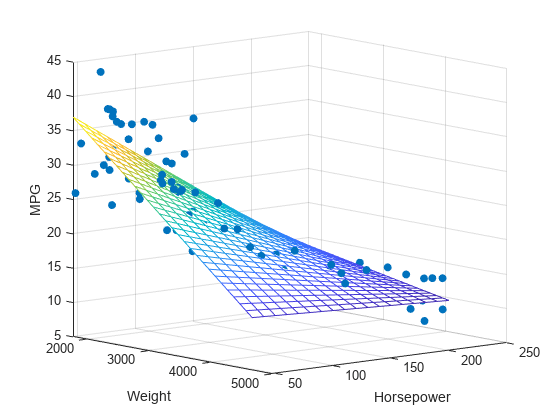
La regresión lineal múltiple es una extensión de la regresión lineal simple que se utiliza cuando hay más de una variable independiente. Se usa para modelar la relación entre dos o más características y una respuesta mediante el ajuste de una ecuación lineal (más extendida que la anterior) a los datos observados.

La forma básica de una ecuación de regresión lineal múltiple con n variables es:

$Y = a + b_1X_1 + b_2X_2 + ... + b_nX_n + e$

Donde:

• $Y$ es la variable dependiente que intentamos predecir o modelar.
• $X_1, X_2, ..., X_n$ son las variables independientes que utilizamos para hacer la predicción.
• $a$ y $b_1, b_2, ..., b_n$ son los coeficientes que queremos que el modelo aprenda.
• $e$ es el error en la predicción comentado anteriormente. Es la diferencia entre el valor real de $Y$ y el valor de $Y$ predicho por el modelo.

La regresión lineal múltiple permite al analista determinar qué variables en particular tienen un impacto significativo sobre la variable dependiente y en qué magnitud. Al igual que la regresión lineal simple, esta regresión hace supuestos de linealidad, normalidad, homoscedasticidad y ausencia de multicolinealidad, y los resultados pueden ser no confiables si estos supuestos se violan.