Probabilidad

Probabilidad

La probabilidad es una medida que describe la posibilidad de que ocurra un evento en particular dentro de un conjunto de posibles eventos. Se expresa en una escala que va desde 0 (indicando que un evento es imposible) hasta 1 (indicando que un evento es cierto). También puede expresarse como un porcentaje entre 0% y 100%.

La probabilidad proporciona un marco para cuantificar la incertidumbre asociada con predicciones, inferencias, decisiones y eventos aleatorios. Para entenderla y calcularla, es esencial comprender los siguientes conceptos:

• Experimento (experiment): Es cualquier acción o procedimiento que puede producir resultados bien definidos. Ejemplo: lanzar un dado.
• Espacio muestral (sample space): Es el conjunto de todos los posibles resultados de un experimento. Para el ejemplo del dado, el espacio muestral es $S = {1, 2, 3, 4, 5, 6}$ (ya que son todas las posibles caras que pueden salirnos al lanzar un dado).
• Evento (event): También llamado suceso, es el subconjunto específico de resultados dentro de un espacio muestral. En nuestro ejemplo, refiriéndonos al evento de obtener un número par se representaría como $E = {2, 4, 6}$ (ya que todos esos números son pares).

La probabilidad de un evento se calcula como la relación entre el número de resultados favorables para ese evento y el número total de resultados en el espacio muestral. Por ejemplo, la probabilidad de obtener un número par al lanzar un dado es:

$P(E) = \frac{3}{6} = 0.5$

Operaciones entre sucesos

Como hemos visto, un suceso (event) es el resultado de un experimento aleatorio y siempre lleva asociada una probabilidad. A menudo puede que nos interese relacionar las probabilidades entre dos sucesos, y esto se lleva a cabo a través de las operaciones entre sucesos.

Unión de sucesos

Es el suceso que tiene lugar si ocurre al menos uno de los dos sucesos. Se denota por $A \cup B$. Por ejemplo, si $A$ es el suceso de obtener un 2 en un lanzamiento de dado y $B$ es el suceso de obtener un 3, entonces $A \cup B$ es el suceso de obtener un 2 o un 3.

Intersección de sucesos

Es el suceso que tiene lugar si ocurren ambos sucesos a la vez. Se denota por $A \cap B$. Por ejemplo, si $A$ es el suceso de obtener un número menor que 4 y $B$ es el suceso de obtener un número par, entonces $A \cap B$ es el suceso de obtener un 2 (porque es par y el único número menor que 4).

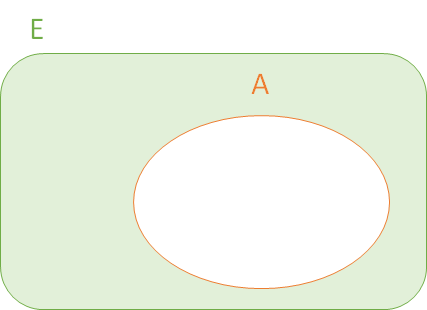
Complemento de un suceso

Es el suceso que tiene lugar si no ocurre el suceso dado. Se denota por $A'$. Por ejemplo, si $A$ es el suceso de obtener un número par al lanzar un dado, entonces $A'$ es el suceso de obtener un número impar.

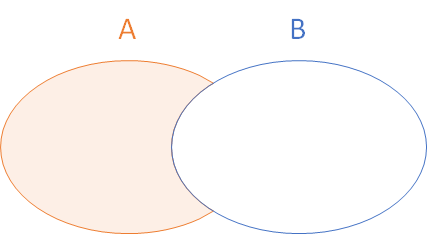
Diferencia entre sucesos

Es el suceso que tiene lugar si ocurre el primer suceso pero no el segundo. Se denota por $A - B$. Por ejemplo, si $A$ es el suceso de obtener un número menor que 4 y $B$ es el suceso de obtener un número par, entonces $A - B$ es el suceso de obtener un 1 o un 3.

Tipos de probabilidad

Existen varios tipos de probabilidad, cada uno adecuado para diferentes contextos o situaciones. Algunos de los más frecuentes son:

1. Probabilidad clásica: Se basa en situaciones donde todos los posibles resultados son igual de probables. Por ejemplo, si lanzamos una moneda al aire, cada cara tiene una probabilidad del 50% de salir.
2. Probabilidad empírica: Se denomina también frecuentista porque se basa en experimentos reales y en observaciones. La probabilidad de un evento se determina observando la frecuencia con la que ocurre después de realizar muchas pruebas o experimentos. Por ejemplo, si al lanzar una moneda 100 veces, cae cara 55 veces, la probabilidad empírica de obtener cara sería de $\frac{55}{100} = 0.55$.
3. Probabilidad subjetiva: Es una estimación basada en la creencia de una persona, a menudo sin base empírica sólida. Por ejemplo, un meteorólogo podría decir que hay un 70% de probabilidad de lluvia basándose en su experiencia e intuición, además de los datos disponibles.
4. Probabilidad condicional: Es la probabilidad de que ocurra un evento $A$ dado que otro evento $B$ ya ha ocurrido. Se denota como $P(A|B)$. Es una de las probabilidades más estudiadas en el campo del Machine Learning, ya que de ella deriva el teorema de Bayes.
5. Probabilidad conjunta: Es la probabilidad de que ocurran dos o más eventos simultáneamente. Se denota como $P(A \cap B)$.

Estos tipos de probabilidad permiten abordar diferentes situaciones y problemas en el campo de la estadística y de la probabilidad, y son fundamentales en muchas aplicaciones, incluyendo la toma de decisiones, el Machine Learning y la investigación científica.

Teorema de Bayes

El teorema de Bayes es una herramienta fundamental en estadística que nos permite actualizar nuestras creencias ante nuevas evidencias.

Imaginemos que tenemos una bolsa con 100 canicas: 30 son rojas y 70 son azules. Si sacamos una canica al azar, la probabilidad de que sea roja es del 30% y la probabilidad de que sea azul es del 70%. Ahora, supongamos que un amigo, sin que lo veamos, elige una canica de la bolsa y nos dice: "La canica que elegí tiene rayas". Si ahora supiéramos que el 50% de las canicas rojas tienen rayas y solo el 10% de las canicas azules las tienen, dada esta nueva información, ¿cuál es la probabilidad de que la canica que nuestro amigo eligió sea roja? Aquí es donde se aplica el teorema de Bayes.

De esta forma podemos calcular de nuevo la probabilidad de que la canica sea roja y tenga rayas, a partir de la nueva información.