Probability

Probability

Probability is a measure that describes the likelihood of a particular event occurring within a set of possible events. It is expressed on a scale ranging from 0 (indicating that an event is impossible) to 1 (indicating that an event is certain). It can also be expressed as a percentage between 0% and 100%.

Probability provides a framework for quantifying the uncertainty associated with predictions, inferences, decisions, and random events. To understand and calculate it, it is essential to understand the following concepts:

• Experiment: Any action or procedure that can produce well-defined results. Example: throwing a dice.
• Sample space: The set of all possible outcomes of an experiment. For the example of the dice, the sample space is $S = {1, 2, 3, 4, 5, 6}$ (since they are all the possible faces that can come out when rolling a dice).
• Event: Also called an occurrence, it is the specific subset of outcomes within a sample space. In our example, referring to the event of getting an even number would be represented as $E = {2, 4, 6}$ (since all those numbers are even).

The probability of an event is calculated as the ratio of the number of favorable outcomes for that event to the total number of outcomes in the sample space. For example, the probability of getting an even number when rolling a dice is:

$P(E) = \frac{3}{6} = 0.5$

Operations between events

As we have seen, an event is the result of a random experiment and always has a probability associated with it. Often, we may be interested in relating the probabilities between two events, and this is done through operations between events.

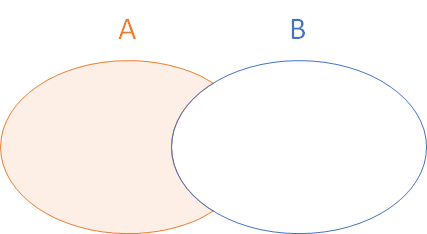
Union of events

The event that occurs if at least one of the two events occurs. It is denoted by $A \cup B$. For example, if $A$ is the event of getting a 2 on a die roll and $B$ is the event of getting a 3, then $A \cup B$ is the event of getting a 2 or a 3.

Intersection of events

The event that occurs if both events occur at the same time. It is denoted by $A \cap B$. For example, if $A$ is the event of getting a number less than 4 and $B$ is the event of getting an even number, then $A \cap B$ is the event of getting a 2 (because it is even and the only number less than 4).

Complement of an event

The event that occurs if the given event does not occur. It is denoted by $A'$. For example, if $A$ is the event of getting an even number by rolling a dice, then $A'$ is the event of getting an odd number.

Difference between events

The event that occurs if the first event occurs but not the second. It is denoted by $A - B$. For example, if $A$ is the event of obtaining a number less than 4 and $B$ is the event of obtaining an even number, then $A - B$ is the event of obtaining a 1 or a 3.

Types of probability

There are several types of probability, each suitable for different contexts or situations. Some of the most common are:

1. Classical probability: This is based on situations where all possible outcomes are equally likely. For example, if we flip a coin, each side has a 50% probability of coming up.
2. Empirical probability: It is also called frequentist because it is based on real experiments and observations. The probability of an event is determined by observing how often it occurs after many trials or experiments. For example, if a coin tossed 100 times, comes up heads 55 times, the empirical probability of getting heads would be $\frac{55}{100} = 0.55$.
3. Subjective probability: This is an estimate based on a person's belief, often without a solid empirical basis. For example, a meteorologist might say there is a 70% chance of rain based on his or her experience and intuition, in addition to the available data.
4. Conditional probability: It is the probability that an event $A$ occurs given that another event $B$ has already occurred. It is denoted as $P(A|B)$. It is one of the most studied probabilities in the field of Machine Learning, since the Bayes' theorem is derived from it.
5. Joint probability: It is the probability that two or more events occur simultaneously. It is denoted as $P(A \cap B)$.

These types of probability allow addressing different situations and problems in the field of statistics and probability, and are fundamental in many applications, including decision-making, Machine Learning, and scientific research.

Bayes' Theorem

Bayes' theorem is a fundamental tool in statistics that allows us to update our beliefs in the face of new evidence.

Let's imagine we have a bag with 100 marbles: 30 are red and 70 are blue. If we draw a marble at random, the probability that it is red is 30%, and the probability that it is blue is 70%. Now, suppose a friend, unseen by us, picks a marble out of the bag and says, "The marble I picked has stripes on it." If we now know that 50% of the red marbles have stripes and only 10% of the blue marbles have stripes, given this new information, what is the probability that the marble our friend chose is red? This is where Bayes' theorem applies.

This way, we can recalculate the probability that the marble is red and has stripes, given the new information.