Boosting de Algoritmos

Boosting

Boosting es una técnica que se utiliza para mejorar el rendimiento de los modelos. La idea esencial detrás del boosting es entrenar una serie de modelos débiles (generalmente árboles de decisión), cada uno de los cuales intenta corregir los errores del anterior.

Estructura

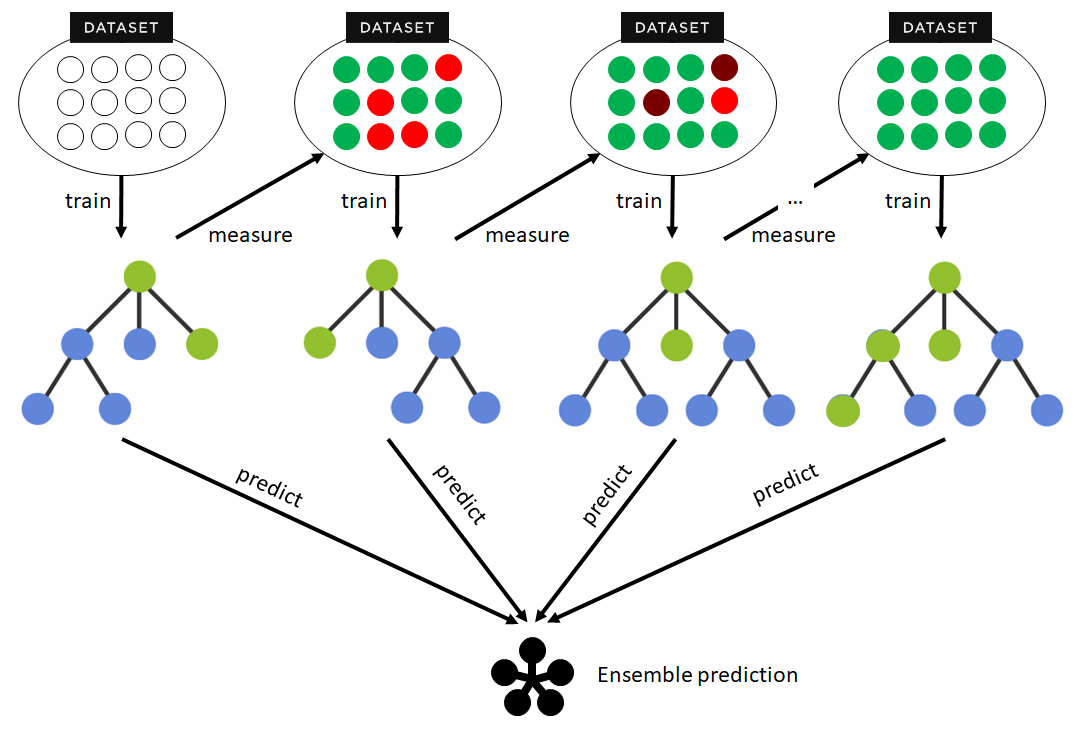
El modelo tiene una estructura secuencial y cada modelo en la secuencia se construye para corregir los errores de su predecesor. La estructura de un algoritmo de boosting sigue un proceso caracterizado con los siguientes pasos:

1. Inicialización. Primero, se asigna un peso inicial a cada instancia (fila) en el conjunto de entrenamiento. Por lo general, estos pesos son iguales para todas las instancias al inicio.
2. Entrenamiento del primer modelo. Se entrena un modelo con los datos de entrenamiento. Este modelo hará algunas predicciones correctas y algunas incorrectas.
3. Cálculo de errores. A continuación, se calcula el error del modelo anterior en función de los pesos anteriores. Las instancias mal clasificadas por este modelo recibirán un mayor peso, de manera que se destacarán en el siguiente paso.
4. Entrenamiento del segundo modelo. Se entrena un nuevo modelo, pero ahora se enfoca más en las instancias con mayor peso (las que el modelo anterior clasificó erróneamente).
5. Iteración. Se repiten los pasos 3 y 4 para un número predefinido de veces, o hasta que se alcance un límite de error aceptable. Cada nuevo modelo se concentra en corregir los errores del modelo anterior.
6. Combinación de los modelos. Tras el fin de las iteraciones, los modelos se combinan a través de una suma ponderada de sus predicciones. Los modelos que tienen un mejor rendimiento (es decir, cometen menos errores en sus predicciones) suelen tener mayor peso en la suma.

Es importante tener en cuenta que el boosting puede ser más susceptible al sobreajuste que otras técnicas si no se controla, dado que cada nuevo modelo está tratando de corregir los errores del anterior y podría terminar adaptándose demasiado a los datos de entrenamiento. Por lo tanto, es crucial tener un buen control de los hiperparámetros y realizar una validación cruzada durante el entrenamiento.

Implementaciones

Existen multitud de implementaciones de este modelo, desde más a menos eficientes, con mayor o menor flexibilidad con respecto a los tipos de datos, según si se utilizan para clasificación o regresión, etcétera. Nosotros nos centraremos en el boosting por gradiente (gradient boosting), que es válido tanto para clasificación como para regresión.

XGBoost

XGBoost (eXtreme Gradient Boosting) es la implementación más eficiente del algoritmo de gradient boosting. Se ha desarrollado buscando rapidez y precisión, y hasta ahora es la mejor implementación, superando en tiempos de entrenamiento a la de sklearn. La reducción de tiempos se debe a que proporciona métodos para paralelizar las tareas, así como flexibilidad a la hora de entrenar el modelo y es más robusto, pudiendo incluir mecanismos de poda de los árboles para ahorrar tiempos de procesamiento. Siempre que la tengamos disponible, esta es la alternativa que se debería utilizar frente a la de sklearn.

En la lectura ejemplificamos cómo utilizar XGBoost, pero aquí proporcionaremos un código simple de muestra para que se vea el uso de sklearn para implementar boosting:

Clasificación

1from sklearn.ensemble import GradientBoostingClassifier
2
3# Carga de los datos de train y test
4# Estos datos deben haber sido normalizados y correctamente tratados en un EDA completo
5
6model = GradientBoostingClassifier(n_estimators = 5, random_state = 42)
7
8model.fit(X_train, y_train)
9
10y_pred = model.predict(y_test)

Regresión

1from sklearn.ensemble import GradientBoostingRegressor
2
3# Carga de los datos de train y test
4# Estos datos deben haber sido normalizados y correctamente tratados en un EDA completo
5
6model = GradientBoostingRegressor(n_estimators = 5, random_state = 42)
7
8model.fit(X_train, y_train)
9
10y_pred = model.predict(y_test)

Hiperparametrización del modelo

Podemos construir un árbol de decisión fácilmente en Python utilizando la librería scikit-learn y las funciones GradientBoostingClassifier y GradientBoostingRegressor. También podemos utilizar una alternativa más eficiente llamada XGBoost para clasificar y hacer regresión con las funciones XGBClassifier y XGBRegressor. Algunos de sus hiperparámetros más importantes y los primeros en los que debemos centrarnos son:

• n_estimators (n_estimators en XGBoost): Este es probablemente el hiperparámetro más importante. Define el número de árboles de decisión en el bosque. En general, un número mayor de árboles aumenta la precisión y hace que las predicciones sean más estables, pero también puede ralentizar considerablemente el tiempo de cálculo.
• learning_rate (learning_rate en XGBoost): La tasa a la cual se acepta el modelo en cada etapa de boosting. Una tasa de aprendizaje más elevada puede llevar a un modelo más complejo, mientras que una tasa más baja requerirá más árboles para obtener el mismo nivel de complejidad.
• loss (objective en XGBoost): La función de pérdida a optimizar (cantidad de errores de clasificación o diferencia con la realidad en regresión).
• subsample (subsample en XGBoost): La fracción de instancias a utilizar para entrenar los modelos. Si es menor que 1.0, entonces cada árbol se entrena con una fracción aleatoria del total de las instancias del dataset de entrenamiento.
• max_depth (max_depth en XGBoost): La profundidad máxima de los árboles. Esto es esencialmente cuántas divisiones puede hacer el árbol antes de hacer una predicción.
• min_samples_split (gamma en XGBoost): El número mínimo de muestras necesarias para dividir un nodo en cada árbol. Si se establece un valor alto, evita que el modelo aprenda relaciones demasiado específicas y, por tanto, ayuda a prevenir el sobreajuste.
• min_samples_leaf (min_child_weight en XGBoost): El número mínimo de muestras que se deben tener en un nodo hoja en cada árbol.
• max_features (colsample_by_level en XGBoost): El número máximo de características a considerar al buscar la mejor división dentro de cada árbol. Por ejemplo, si tenemos 10 características, podemos elegir que cada árbol considere solo un subconjunto de ellas al decidir dónde dividir.

Como podemos ver, solo los cuatro primeros hiperparámetros hacen referencia al boosting, mientras que el resto eran relacionados a los árboles de decisión. Otro hiperparámetro muy importante es el random_state, que controla la semilla de generación aleatoria. Este atributo es crucial para asegurar la replicabilidad.

Boosting vs Random forest

Boosting y random forest son dos técnicas de Machine Learning que combinan múltiples modelos para mejorar la precisión y estabilidad de las predicciones. Aunque ambas técnicas se basan en la idea de ensamblar varios modelos, tienen algunas diferencias clave.

	Boosting	Random forest
Estrategia de ensamble	Los modelos se entrenan de forma secuencial, cada uno intenta corregir los errores del modelo anterior.	Los modelos se entrenan de forma independiente, cada uno con una muestra aleatoria de los datos
Capacidad de modelado	Puede capturar relaciones complejas y no lineales en los datos.	Más "plano" y menor capacidad de capturar relaciones complejas y no lineales.
Prevención de sobreajuste	Puede ser más propenso al sobreajuste, especialmente con ruido o valores atípicos en los datos.	Generalmente menos propenso al sobreajuste.
Rendimiento y precisión	Tiende a tener un mayor rendimiento en términos de precisión, pero puede ser más sensible a los hiperparámetros.	Puede tener menor rendimiento de precisión, pero es más robusto a las variaciones de hiperparámetros.
Tiempo de entrenamiento	Puede ser más lento para entrenar porque los modelos deben ser entrenados secuencialmente, uno detrás de otro.	Puede ser más rápido para entrenar porque todos los modelos pueden ser entrenados en paralelo.

Estas diferencias fundamentales entre los dos modelos hacen que sean más o menos indicados según la situación y las características de los datos. Sin embargo, para dejarlo más claro, podemos establecer algunos criterios basados en las características de los datos que podríamos considerar al elegir boosting y random forest:

	Boosting	Random forest
Tamaño del conjunto de datos	Funciona mejor con grandes conjuntos donde la mejora en rendimiento puede compensar el tiempo adicional de entrenamiento y afinación.	Funciona bien tanto con conjuntos pequeños como grandes, aunque puede ser preferible para conjuntos de datos pequeños debido a su eficiencia.
Número de predictoras	Funciona mejor con grandes volúmenes de predictoras, ya que puede captar interacciones complejas.	Funciona bien con grandes volúmenes de predictoras.
Distribuciones	Puede manejar distribuciones no usuales, ya que es bueno interpretando relaciones no lineales complejas entre los datos.	Es robusto a las distribuciones usuales, pero puede tener problemas para modelar relaciones no lineales complejas.
Outliers	Muy sensible a valores atípicos.	Robusto a valores atípicos gracias a su naturaleza basada en particiones.

La elección entre boosting y random forest depende del problema específico y del conjunto de datos con el que estemos trabajando, pero estas normas generales son un buen punto de partida para encarar los diferentes problemas del mundo real.