Integrales y Derivadas

Cálculo

El cálculo, el álgebra lineal y la probabilidad son los "lenguajes" en los que se escribe Machine Learning. Aprender estos temas proporcionará una comprensión más profunda de la mecánica algorítmica subyacente y permitirá el desarrollo de nuevos algoritmos, que en última instancia pueden implementarse como estrategias comerciales cuantitativas más sofisticadas.

El cálculo es el estudio matemático de cambio continuo. Necesitas saber un poco de cálculo básico para entender mejor los conceptos de Machine Learning y el comportamiento de las funciones.

Vamos a hablar sobre las tres grandes ideas del Cálculo: Integrales, Derivadas, y el hecho de que son opuestos.

Derivadas tratan de comprender cómo cambian las funciones con el tiempo.

Integrales te permiten calcular el total de una cantidad que se acumula durante un período de tiempo.

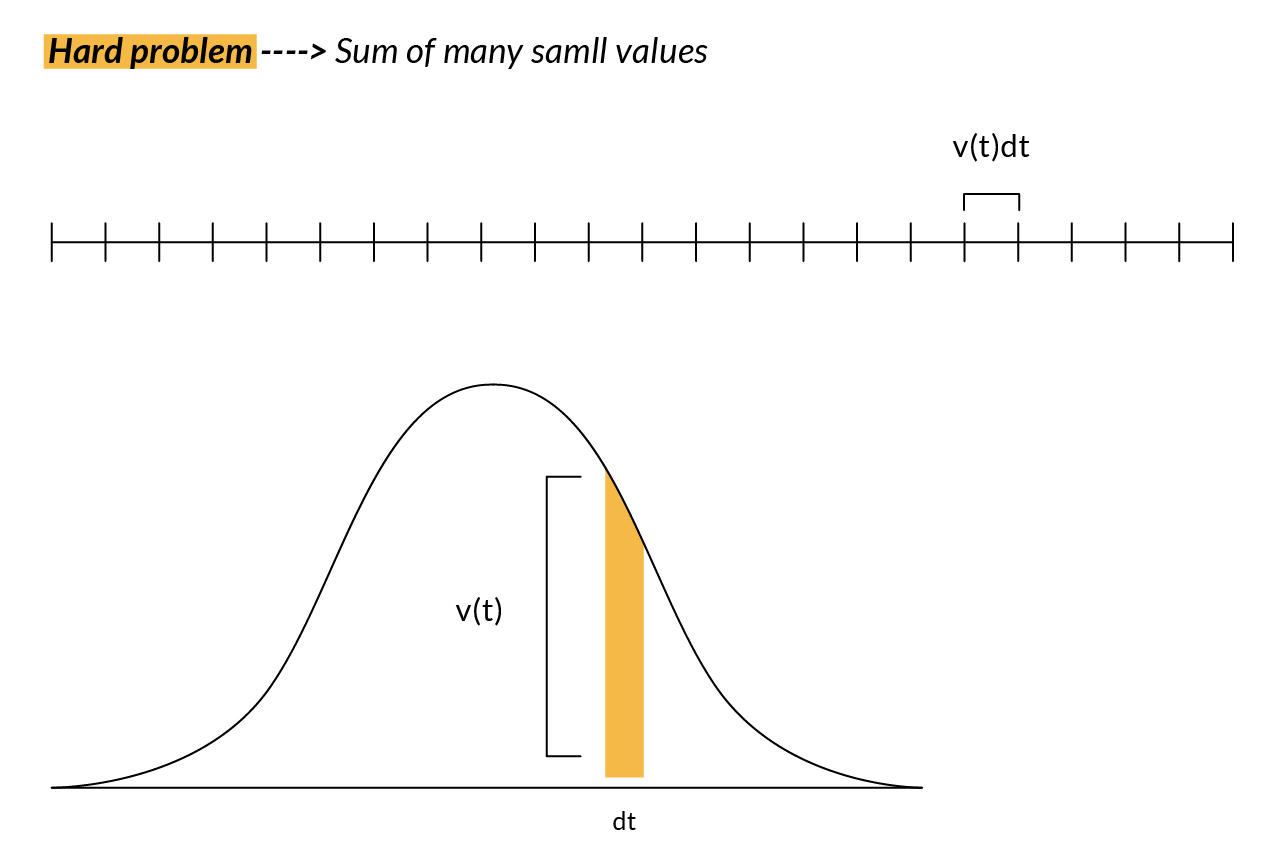
Entonces, pensando como un ingeniero, no solo nos importa encontrar las respuestas. Nos preocupamos por desarrollar herramientas y técnicas de resolución de problemas. Un gran tema en Cálculo es que la aproximación usando muchas piezas más pequeñas nos da la flexibilidad de reformular nuestra pregunta original en algo más simple. Un gran problema es por un lado, la suma de muchos valores pequeños, pero por otro lado, esa suma también se aproxima al área bajo un gráfico.

Integrales

Por ejemplo, si quisieramos saber cuan lejos ha caminado una persona basada en su velocidad en cada punto del tiempo, podemos dividirlo por muchos puntos en el tiempo y multiplicar la velocidad en cada instante (t) por un pequeño cambio en el tiempo (dt) para obtener la distancia más pequeña correspondiente recorrida en ese periodo más pequeño.

Muchos de estos tipos de problemas terminan siendo equivalentes a encontrar el área debajo de un gráfico. El propósito de las pequeñas aproximaciones es que nos permite replantear el problema de qué tan lejos ha caminado la persona en la pregunta de encontrar el área bajo cierta curva.

Entonces, ya habiendo resuelto el problema reformulándolo como un área debajo de un gráfico, puedes empezar a pensar sobre como conseguir el área debajo de otros gráficos. Ahora veamos un gráfico diferente.

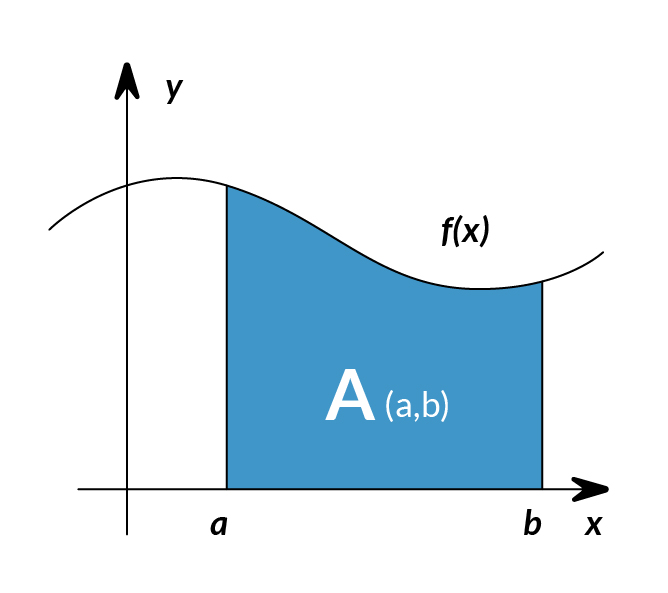
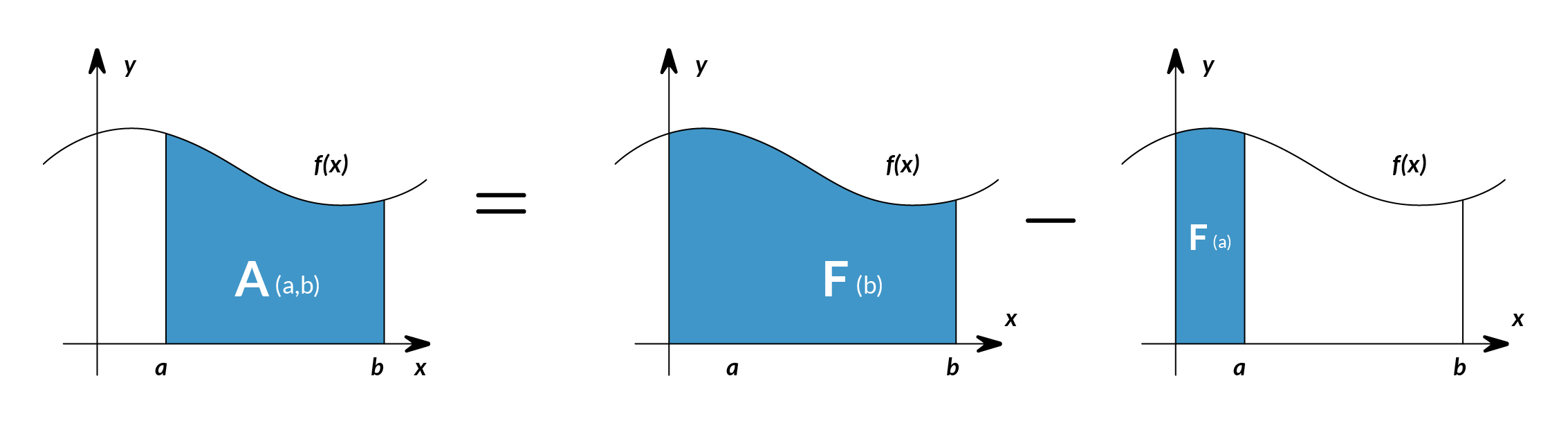
la integral de $f(x)$ corresponde al cálculo del área bajo la gráfica de $f(x)$. El área bajo $f(x)$ entre los puntos $x = a$ y $x = b$ se denota de la siguiente manera:

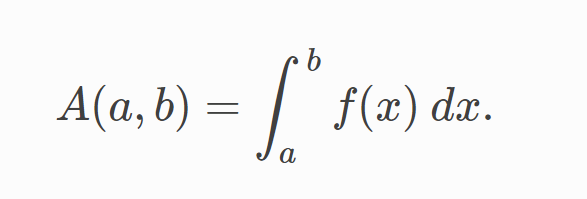
El área $A(a,b)$ está delimitada por la función $f(x)$ desde arriba, por el eje x desde abajo y por dos líneas verticales en $x = a$ y $x = b$. Esos dos puntos $x = a$ y $x = b$ se denotan los límites de integración. El signo $∫$ proviene de la palabra en latín "summa". La integral es la suma de los valores de $f(x)$ entre los dos límites de la integración.

El área debajo de $f(x)$ entre $x = a$ y $x = b$ se obtiene calculando el cambio en la función integral de la siguiente manera:

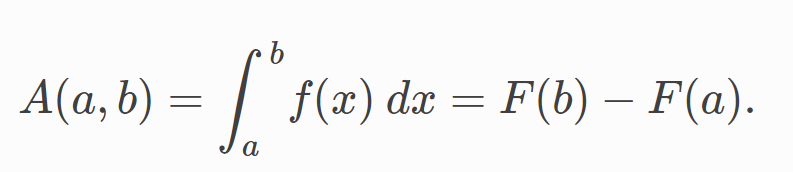
Podemos aproximar el área total debajo de la función $f(x)$ entre $x = a$ y $x = b$ separando el gráfico en pequeñas tiras rectangulares verticales de width $h$, luego sumando las áreas de esas tiras rectangulares. La figura debajo enseña cómo calcular el área bajo $f(x) = x2$ entre $x = 3$ y $x = 6$ aproximándola como seis franjas rectangulares de width $h = 0,5$.

Para recapitular, $A(x)$ que da el área bajo el gráfico de x2 entre un punto fijo a la izquierda y un punto variable a la derecha nos da un claro panorama de que muchos problemas prácticos que se pueden aproximar sumando un gran número de cosas pequeñas se pueden replantear como una pregunta sobre el área bajo cierta curva.

Derivadas

¿Qué es una derivada?

Una derivada se puede definir de dos maneras:

1. Tasa de cambio instantáneo (Física).

2. La pendiente de una línea en un punto específico (Geometría)

Nosotros vamos a usar la definición de geometría para una explicación mas sencilla.

La pendiente representa la inclinación de una recta. Significa: ¿Cuánto cambia $y$ (o $f(x)$) dado un cambio específico en $x$?

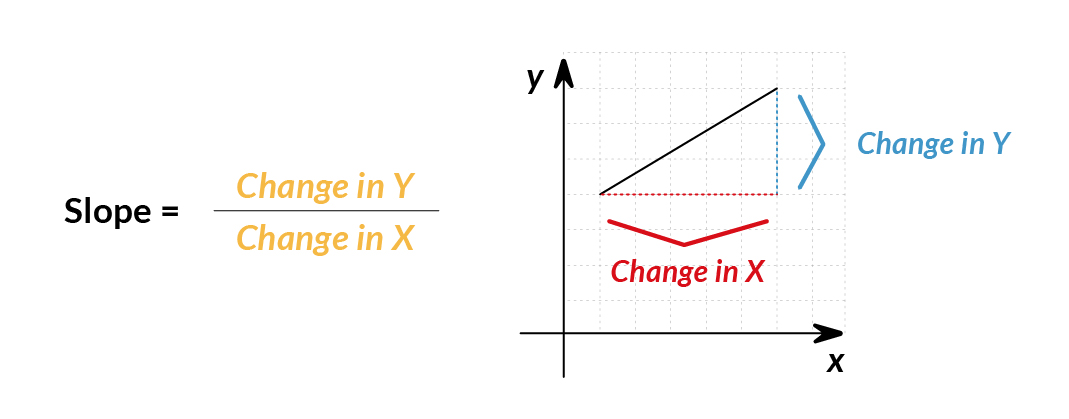
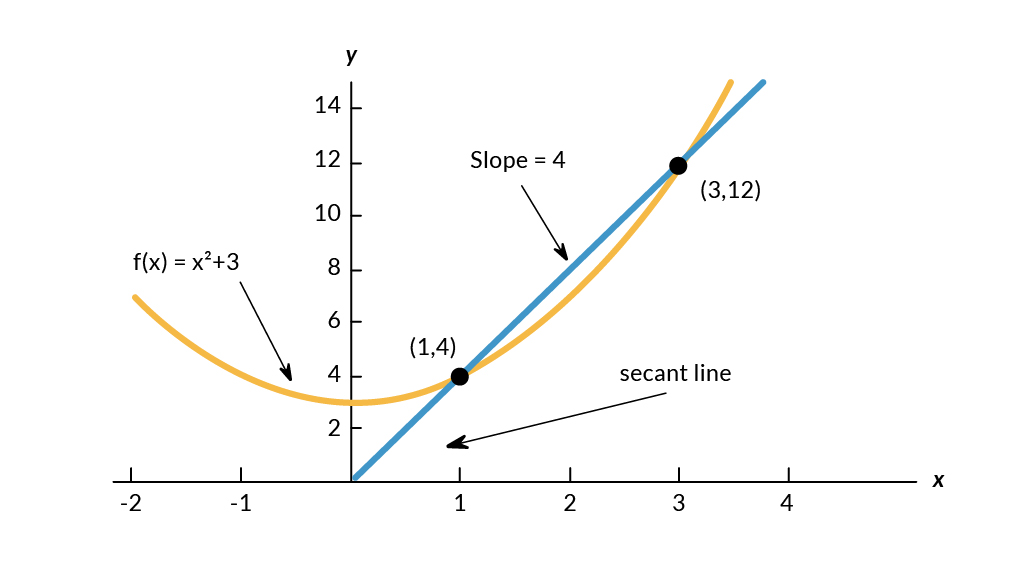
La pendiente entre $(1,4)$ y $(3,12)$ sería:

slope= $\frac{(y2−y1)}{(x2−x1)}$ = $\frac{(12-4)}{(3-1)} = 4$

Casos de usos de Machine

Machine learning usa derivadas en la optimización de problemas. Los algoritmos de optimización como el descenso de gradiente utilizan derivadas para decidir si aumentar o disminuir los pesos para maximizar o minimizar algún objetivo (por ejemplo, la precisión de un modelo o las funciones de error). Las derivadas también nos ayudan a aproximar funciones no lineales como funciones lineales (líneas tangentes), que tienen pendientes constantes. Con una pendiente constante, podemos decidir si subir o bajar la pendiente (aumentar o disminuir nuestros pesos) para acercarnos al valor objetivo (class label).

References:

https://en.wikipedia.org/wiki/Calculus

https://www.youtube.com/watch?v=WUvTyaaNkzM

https://ml-cheatsheet.readthedocs.io/en/latest/calculus.html#introduction-1