Usando javascript para ordenar una lista

Ordenar es una tarea costosa para la CPU de la computadora, depende de la cantidad de datos y la forma en que están organizados los datos inicialmente. Esta combinación de posibilidades hizo que los desarrolladores crearan varias soluciones algorítmicas que se pueden aplicar a cada lenguaje de programación.

P: Busqué en Google y encontré un .sort (), entonces, ¿por qué debería hacerlo manualmente?

R: Ordenar algoritmos es una de las primeras lecciones en Informática, ya que te ayuda a pensar como un computador. Es una gran práctica comprender completamente los conceptos de algoritmos y códigos.

P: ¿Qué tipos de algoritmos para ordenar existen?

R: Hay más de los que podemos contar, los 10 más populares son:

Algoritmo bubble-sort

Es el más simple de los algoritmos para ordenar. Intercambia repetidamente elementos adyacentes para organizarlos de forma ascendente, el algoritmo tiene un "wall" o muro que representa la última posición que se va a comparar, el muro sigue moviéndose de izquierda a derecha, reduciendo el tamaño de comparación hasta que se ordena la lista completa.

En Javascript:

1const bubbleSort = (arr) => {
2    let wall = arr.length - 1; //iniciamos el wall o muro al final del array
3    while (wall > 0){
4        let index = 0;
5        while (index < wall) {
6          //comparar las posiciones adyacentes, si la correcta es más grande, tenemos que intercambiar
7          if (arr[index] > arr[index + 1]) { 
8            let aux = arr[index]; 
9            arr[index] = arr[index + 1];
10            arr[index + 1] = aux;
11          }
12          index++;
13        }
14        wall--; //disminuir la pared para optimizar
15    }
16	return arr;
17};

📺 En este enlace, encontrarás una muy buen video de 2 minutos con una explicación.

📺 Aquí hay un verdadero grupo extraño de búlgaros bailando el algoritmo bubble-sort.

Ordenando con selection

Selection también tiene un muro, pero en este caso, marca el comienzo del bucle, el algoritmo busca el elemento más pequeño y lo intercambia con el inicial, luego mueve el muro una posición hacia la derecha para no ver de nuevo ese mismo artículo.

En javascript

1const selectSort = (arr) => {
2    let min = 0;
3    while (min < arr.length-1){
4        for(let i = min+1; i < arr.length-1; i++) {
5          if (arr[min] > arr[i]) {
6            let aux = arr[min];
7            arr[min] = arr[i];
8            arr[i] = aux;
9          }
10        }
11        min++;
12    }
13	return arr;
14};

📺 En este enlace, encontrarás una muy buena explicación en un video de 3 minutos sobre el algoritmo de clasificación por selección.

Ordenando con el Cocktail Shaker

Cocktail Shaker funciona en ambos frentes al mismo tiempo: busca el de mayor valor escaneando de izquierda a derecha y también el más pequeño cuando vuelve de derecha a izquierda. Tiene 2 muros (uno para cada lado de la lista), y ambos muros siguen encogiéndose hasta que chocan entre sí, cuando eso sucede, el array está completamente ordenado.

En javascript:

1const shakerSort = (arr) => {
2  let max = arr.length - 1;
3  let min = 0;
4  while(min < max){
5  	let biggest = min;
6    let smallest = max;
7    //
8  	for (var i = min; i <= max; i++) if(arr[biggest] < arr[i]) biggest = i;
9    if(max != biggest){ //swap the items
10    	let aux = arr[max]; arr[max] = arr[biggest]; arr[biggest] = aux;
11    }
12    max--;
13    for (var j = max; j >= min; j--) if(arr[smallest] > arr[j]) smallest = j;
14    if(min != smallest){ //swap the items
15    	let aux2 = arr[min]; arr[min] = arr[smallest]; arr[smallest] = aux2;
16    }
17    min++;
18  }  
19  return arr;
20}

📺 En este enlace, encontrarás una muy buena explicación en un video de 3 minutos sobre el algoritmo para ordenar Cocktail Shaker.

Ordenando con Insertion

Ordenar con Insertion implica pasar por una pila, tomar un elemento, compararlo con el primero, intercambiar lugares si un elemento es más grande que otro y continuar este proceso hasta que el elemento mínimo se encuentre en la ubicación correcta.

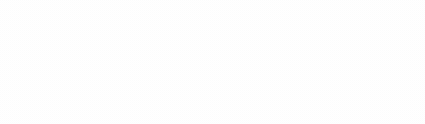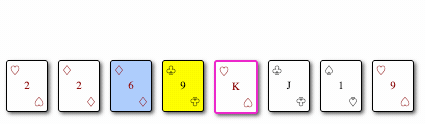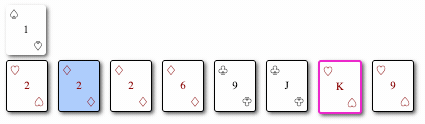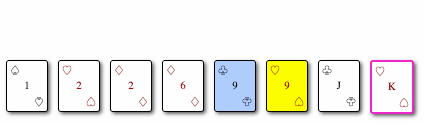En javascript:

1const insertionSort = (arr) => {
2    for (let i = 1; i < arr.length; i++) {
3	    let key = arr[i];
4        let j = i - 1;
5        while (j >= 0 && arr[j].num > key.num) {
6            arr[j + 1] = arr[j];
7            j--;
8        }
9        arr[j + 1] = key;
10    }
11    return arr;
12};

📺 En este enlace, encontrarás una muy buena explicación en un video de 3 minutos sobre el algoritmo para ordenar Insertion.

Ordenando con Merge

Merge es un algoritmo más difícil porque usa recursividad. Es un ejemplo de un algoritmo para ordenar del tipo dividir y conquistar, divide el array desordenado en dos partes y luego recursivamente aplica merge a estos arrays a estos sub-array hasta quedar con un montón de arrays con un solo elemento. Luego, compara los arrays de un solo elemento entre sí antes de combinarlos en un array ordenado de dos elementos (y así sucesivamente). Terminará con una solo array ordenado de longitud n.

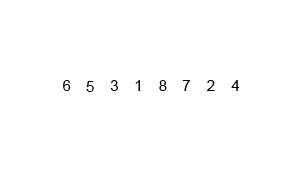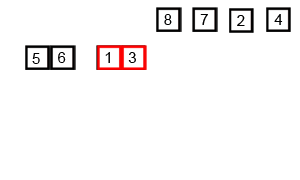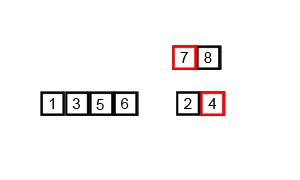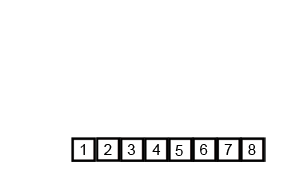
📺 En este enlace, encontrarás una muy buena explicación en un video de 4 minutos sobre el algoritmo de Merge

Ordenando con quicksort

Utiliza la misma estrategia de "divide y vencerás" para obtener las mismas ventajas. Primero selecciona un valor, que se llama el valor de pivote. La función del valor pivote es ayudar a dividir la lista. La posición actual donde el valor pivote pertenece a la lista final ordenada, comúnmente llamada punto de división, se usará para dividir la lista para las llamadas subsiguientes a la ordenación rápida.

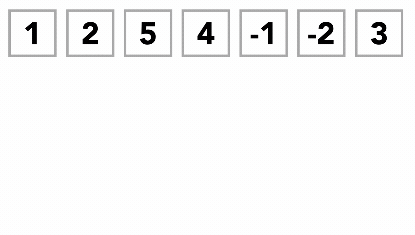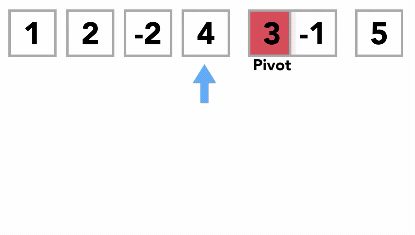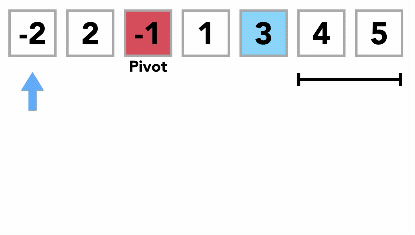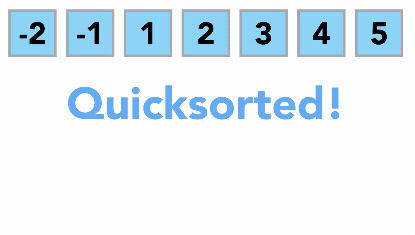
La partición comienza al ubicar dos marcadores de posición, llamémoslos leftmark y rightmark, al principio y al final de los elementos restantes de la lista (posiciones 1 y 8). El objetivo del proceso de partición es mover los elementos que están en el lado incorrecto con respecto al valor de pivote y al mismo tiempo converger en el punto de división.

Comenzamos incrementando leftmark hasta que localizamos un valor que es mayor que el valor de pivote. Luego disminuimos rightmark hasta que encontramos un valor que es menor que el valor de pivote. En este punto, hemos descubierto dos elementos que están fuera de lugar con respecto al punto de división final. Para nuestro ejemplo, esto ocurre en 93 y 20. Ahora podemos intercambiar estos dos elementos y luego repetir el proceso nuevamente.

Cuando rightmark se vuelve menor que leftmark, paramos. La posición de rightmark es ahora el punto de división. El valor de pivote se puede intercambiar con el contenido del punto de división y el valor de pivote ahora está en su lugar. Además, todos los elementos a la izquierda del punto de división son menores que el valor de pivote, y todos los elementos a la derecha del punto de división son mayores que el valor de pivote. La lista ahora se puede dividir en el punto de división y la ordenación rápida se puede invocar recursivamente en las dos mitades.

La función quickSort invoca una función recursiva, quickSortHelper. quickSortHelper comienza con el mismo caso base que Merge. Si la longitud de la lista es menor o igual a uno, ya está ordenada. Si es mayor, puede particionarse y ordenarse recursivamente. La función partition implementa el proceso descrito anteriormente.

📺 En este enlace, encontrarás una muy buena explicación de video de 4 minutos sobre el algoritmo de clasificación rápida.

Recursos Adicionales

Aquí hay otra lista con todos los algoritmos más utilizados: https://codepen.io/msurguy/pen/fBDJA

66/5000 Aquí hay un punto de referencia en la vida real de los principales algoritmos para ordenar: https://codepen.io/villa7/pen/LyLVbj